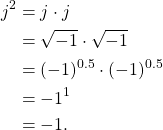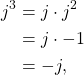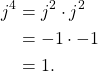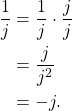Table of Contents
Introduction
The mathematics of DSP and complex numbers can be confounding.
Understanding how ![]() was difficult when I first started my DSP education and it’s still not something I fully grasp. When starting out in your DSP education sometimes it is enough to simply understanding how the tools and procedures are applied, rather than how they are derived.
was difficult when I first started my DSP education and it’s still not something I fully grasp. When starting out in your DSP education sometimes it is enough to simply understanding how the tools and procedures are applied, rather than how they are derived.
Personally, early in my career I accepted the fact that ![]() is true and useful, along with a host of other equations. Over many years of experience in the classroom and in the laboratory I have build some intuition around the mathematics and can apply them appropriately. But it all started with understanding the mathematical rules of complex numbers.
is true and useful, along with a host of other equations. Over many years of experience in the classroom and in the laboratory I have build some intuition around the mathematics and can apply them appropriately. But it all started with understanding the mathematical rules of complex numbers.
More posts on complex numbers:
Square Root of -1
Cartesian Form
Cartesian form is one way to represent complex numbers in a form similar to two dimensional vectors. Cartesian form is the default representation used in computing systems. An example of a two dimensional vector ![]() is given by
is given by
(7) ![]()
where ![]() and
and ![]() are unit vectors. The values c and d are independent of one another because the two unit vectors
are unit vectors. The values c and d are independent of one another because the two unit vectors ![]() and
and ![]() are orthogonal to one another. An example of a two-dimensional vector is given in Figure 1.
are orthogonal to one another. An example of a two-dimensional vector is given in Figure 1.
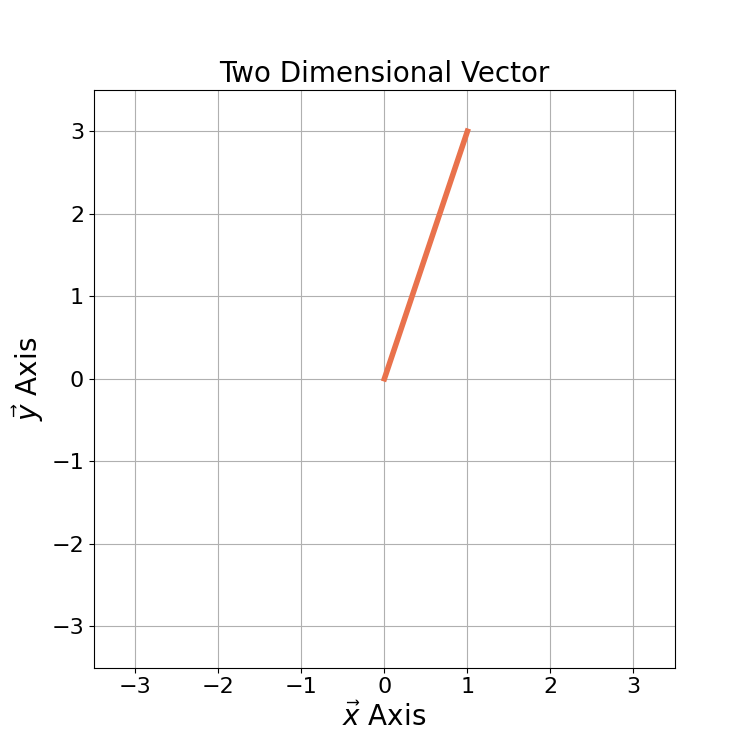
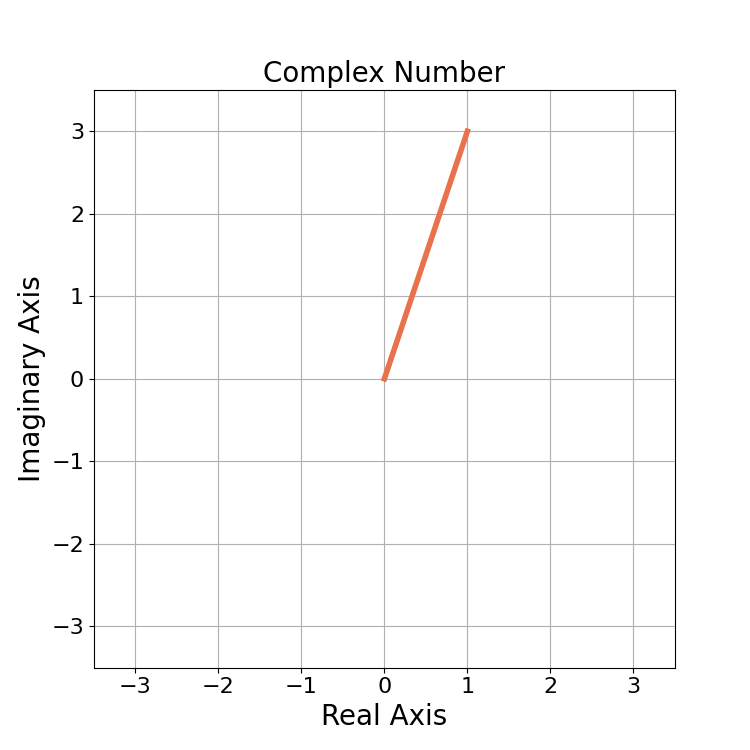
Complex numbers are similar to two-dimensional linear vectors but with additional mathematic relationships. Complex numbers are made of real and imaginary components. For the complex number c,
(8) ![]()
a is the real component and b is the imaginary component. Where the unit vectors ![]() and
and ![]() are made explicit in (7), the unit vector for a is implied and the unit vector for b is j. Figure 2 gives an example of a complex number plotted in the complex domain.
are made explicit in (7), the unit vector for a is implied and the unit vector for b is j. Figure 2 gives an example of a complex number plotted in the complex domain.
Magnitude
The magnitude of a complex number is it’s length in the complex domain,
(9) 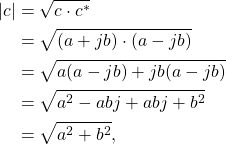
which is analogous to the Euclidean distance of a 2D vector.
For example, the magnitude of ![]() from Figure 2 is
from Figure 2 is
(10) 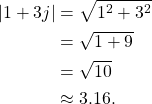
Magnitude-Squared
The magnitude-squared tends to be found in DSP concepts such as energy and power. The magnitude-squared is the square of the magnitude,
(11) 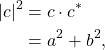
where ![]() . For example, the magnitude-squared of
. For example, the magnitude-squared of ![]() from Figure 2 is
from Figure 2 is
(12) 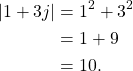
Angle and Phase
The angle or phase of a complex number is its angular distance from 0 degrees, which is 3 o’clock on a clock face. The angle also describes the relationship between the sine and cosine component of a complex exponential if the complex number was treated as the hypotenuse of a triangle.
Mathematically the arctangent is used to calculate the angle of a complex number ![]() where
where
(13) ![]()
The ![]() has a phase ambiguity due the division of
has a phase ambiguity due the division of ![]() . For example, the same angle is calculated when
. For example, the same angle is calculated when ![]() and
and ![]() ,
,
(14) ![]()
(15) 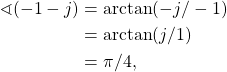
although visually it can be seen in Figure 3 that the angles are not the same.
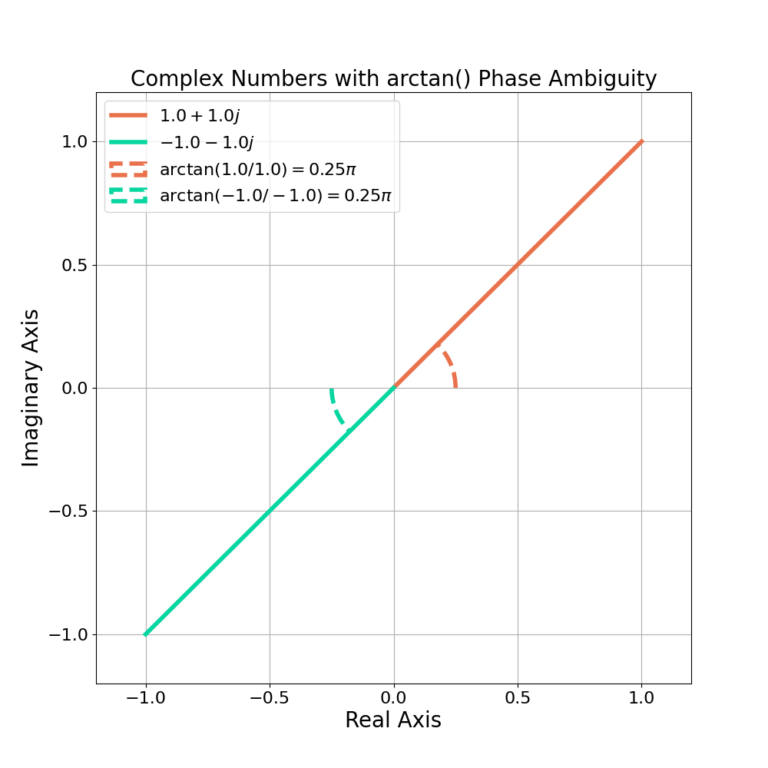
The phase ambiguity is resolved in software by treating the real and imaginary components as separate inputs as in MATLAB’s atan2() function or NumPy’s arctan2(). For example, using arctan2() is given in the following code snippet:
import numpy as np
c = 1 + 1j
print( np.arctan2( np.imag(c), np.real(c) ) )
c = -1 - 1j
print( np.arctan2( np.imag(c), np.real(c) ) )
By convention the angle is measured from 0 degrees, and therefore
(16) ![]()
An example of angles plotted on ![]() is given in Figure 4.
is given in Figure 4.
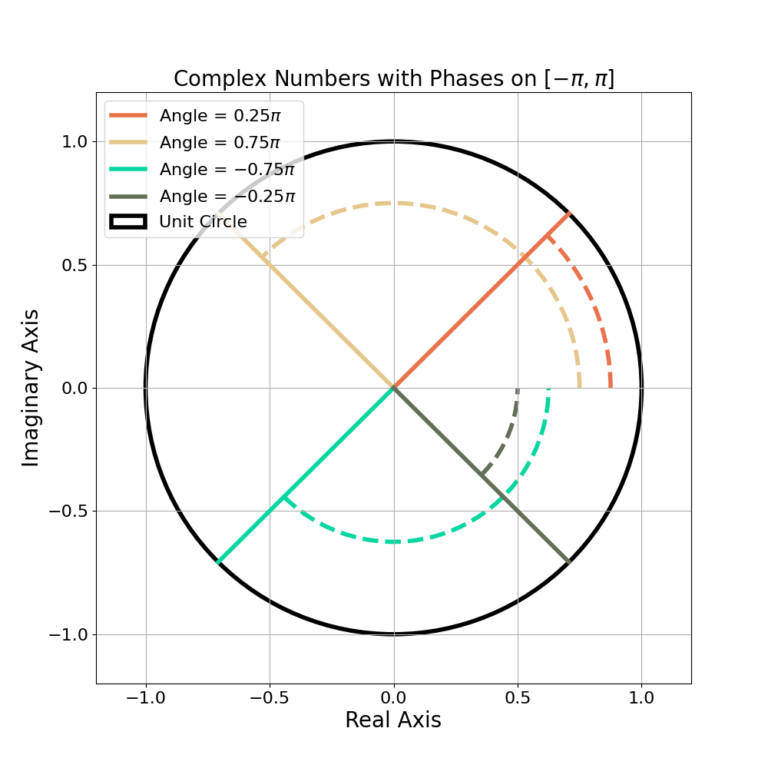
The angle is periodic in ![]() ,
,
(17) ![]()
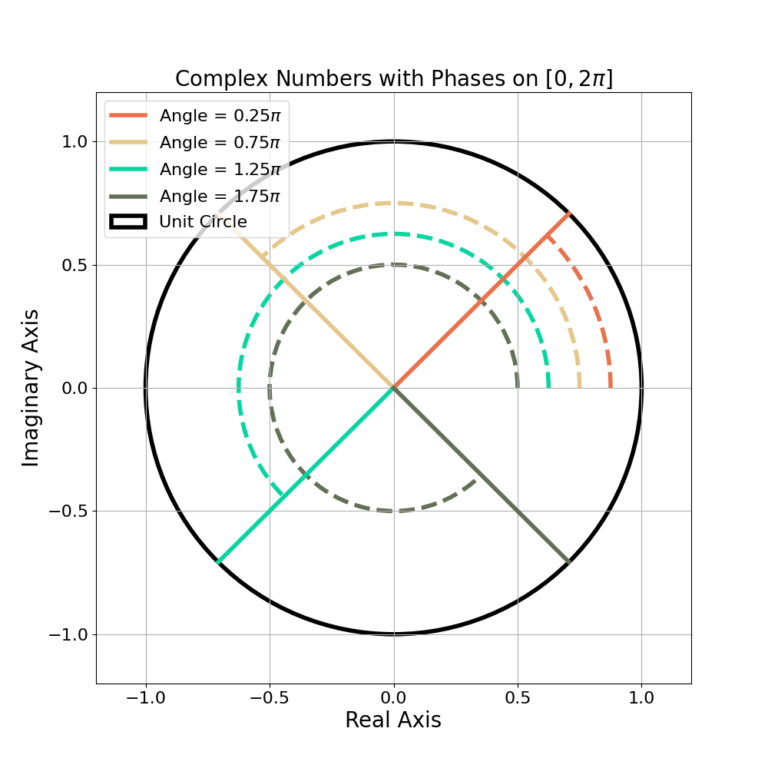
and may also be represented by
(18) ![]()
An example of angles plotted on ![]() is given in Figure 5.
is given in Figure 5.
Polar
Polar form is most commonly used mathematically (pen and paper) due to its simplified multiplication. Almost all useful DSP functions require complex multiplication and therefore the polar form is the most common when working through the mathematics manually.
The polar form of complex number c given by
(19) ![]()
where A is the amplitude and ![]() is the phase. The complex number
is the phase. The complex number ![]() can be represented in polar form by
can be represented in polar form by
(20) 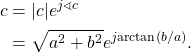
Conjugation
Conjugation ![]() negates the imaginary element of a complex number such that
negates the imaginary element of a complex number such that
(21) ![]()
For ![]() , the conjugate is given by
, the conjugate is given by
(22) ![]()
Conjugation is also the mirroring of c across the imaginary axis. Figure 6 gives an example of a complex number and it’s conjugate in the complex domain.
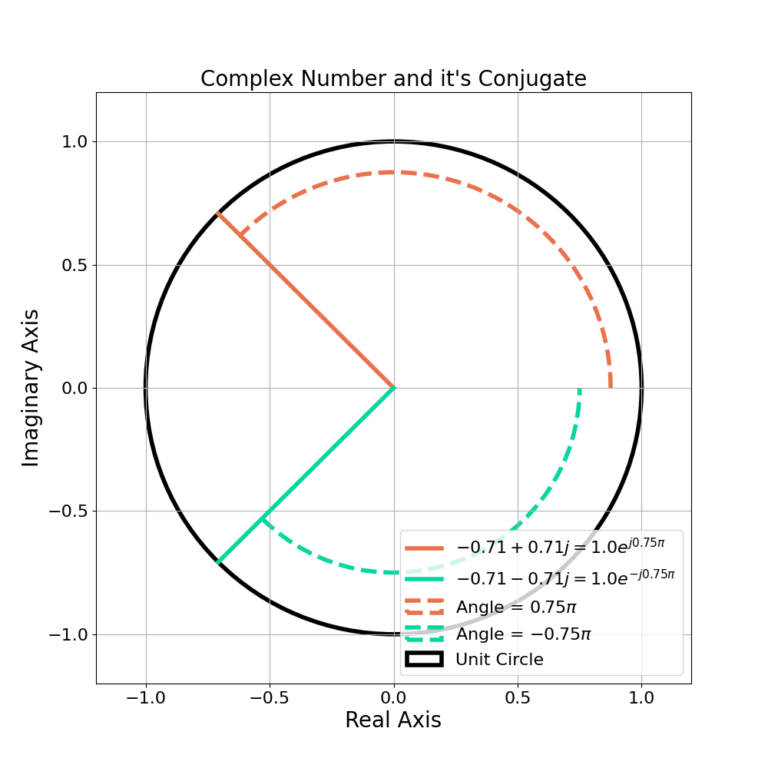
The conjugation operation does not effect the magnitude of a complex number ![]() ,
,
(23) 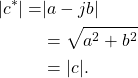
Conjugation negates the angle of a complex number,
(24) ![]()
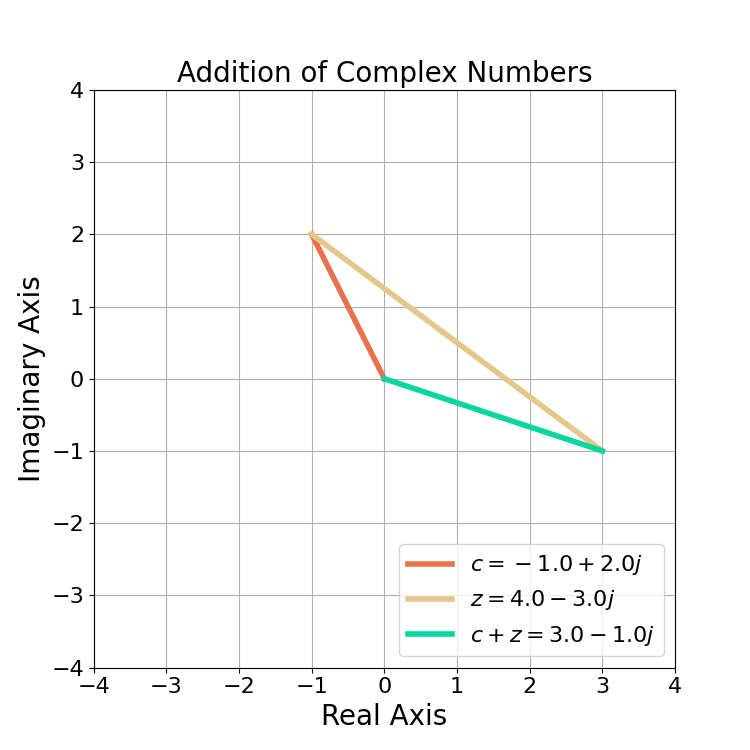
Addition
The addition of complex numbers c and z,
(25) ![]()
(26) ![]()
is given by
(27) ![]()
The addition of complex numbers is most easily done with Cartesian form rather than polar form. Adding complex numbers sums the real and imaginary portions separately (as they are orthogonal to one another) which can be visualized in Figure 7.
Multiplication
The multiplication of complex numbers c and z,
(28) ![]()
(29) ![]()
is given by
(30) 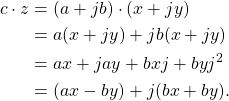
The multiplication of (30) is clunky due to the distribution of the multiplication across multiple terms and can be simplified by converting both terms to polar first.
The multiplication of two complex numbers ![]() and
and ![]() is given by
is given by
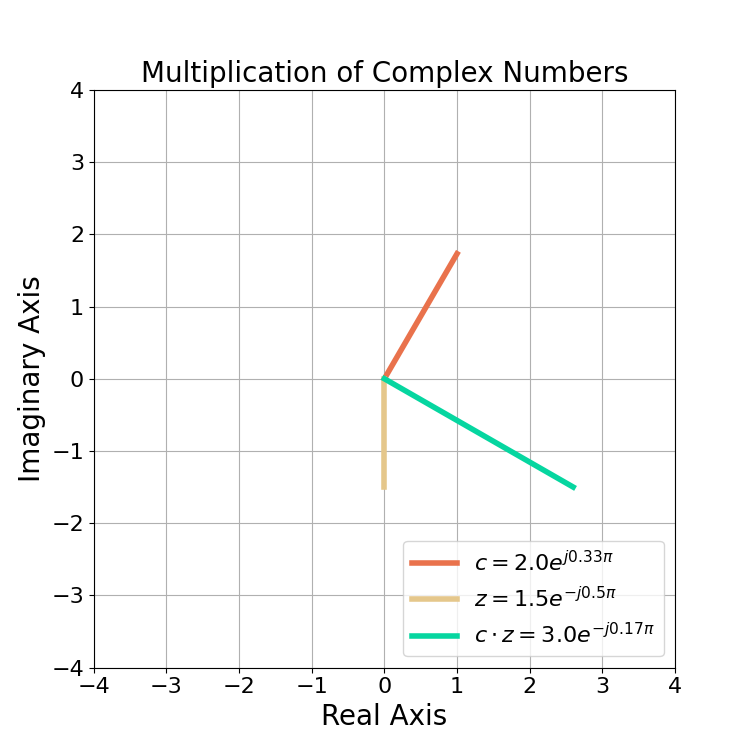
(31) ![]()
Figure 8 gives an example for ![]() and
and ![]() where
where ![]()
Conclusion
Complex mathematics can be confusing, I know it was for me when first starting out in my career. Understanding how to apply the rules of complex math in the classroom allowed me to experiment and apply those rules to building DSP algorithms in the laboratory. Over the course of many years I was able to develop intuition about complex mathematics that allows for the development of new algorithms. But it all started by being comfortable in my uncomfortableness of not completely understanding why they all worked, but knowing enough to be able to apply the mathematics.
Check out more posts on complex numbers:
![Figure 3: The complex sinusoid e(j2 pi (2/4) n) only contains energy at X[2].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/8136-featured-125x100.png)