Wave Walker DSP

DSP Algorithms for RF Systems

Most Popular

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

bookCover2Ed
examples1
examples2
eulersFormula
radians
negativeFrequency
adding
posNegAngles
complexSinusoidPhase
Designing an FIR High Pass Filter with Remez
September 23, 2021

Table of Contents

Introduction

While low-pass filtering (LPF) is ubiquitous high pass filters (HPF) can be needed depending on the RF environment or for specific algorithms. The previous post FIR Low Pass Filter Design with Remez demonstrated how to use the remez() function in the SciPy package to design LPF filter weights. The following blog will demonstrate how to use remez() to design a high pass filter as well as designing LPF filters and upconverting them.

Additional examples for Remez filter design can be found in the SciPy documentation under “Examples”.

More blog posts on filter design:

Design a High Pass Filter with Remez

A HPF can be designed directly with remez() using the following code:

import scipy.signal
filterLength = 21
cutoff = 0.375
transBand = 0.1
fPass = cutoff - (transBand/2)
fStop = cutoff + (transBand/2)
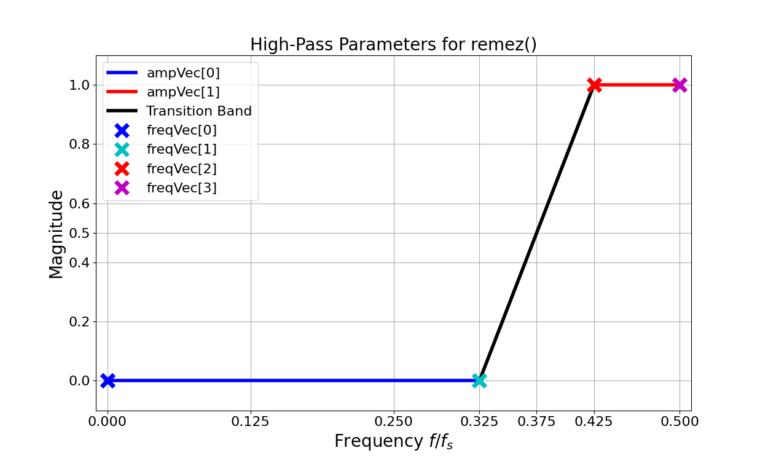
freqVec = [0, fPass, fStop, 0.5]
ampVec = [0, 1]
HPFRemez = scipy.signal.remez(filterLength,freqVec,ampVec)

The design is similar to that of the LPF discussed in this blog post with the differences being in the cutoff frequency and amplitude vector.

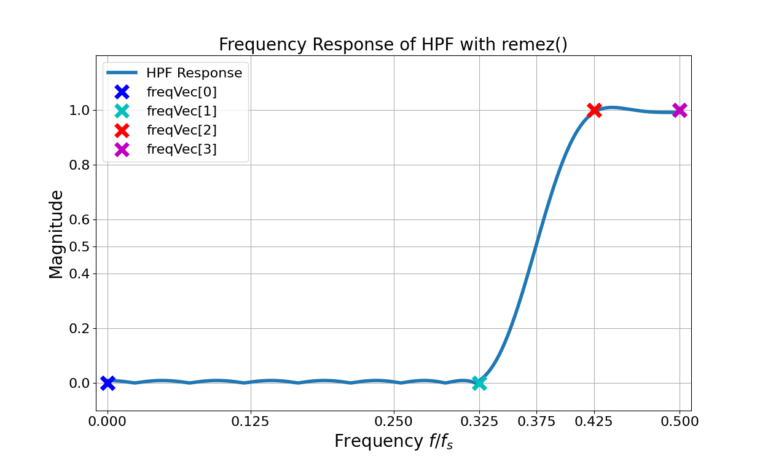
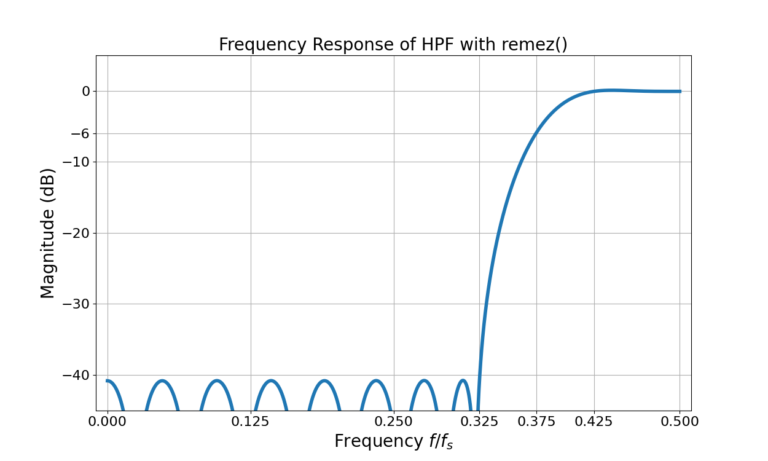
The HPF parameters passed into the remez() function are given in Figure 1, the resulting frequency response in Figure 2 and the magnitude in dB in Figure 3.

Figure 1: The parameters for remez() for designing an example HPF.
Figure 2: The magnitude of the HPF frequency response.
Figure 2: The magnitude of the HPF frequency response.
Figure 3: The HPF frequency response in dB.
Figure 3: The HPF frequency response in dB.

Upconvert Low Pass Filter to High Pass Filter

An alternative to designing a HPF directly is to design an LPF and then upconvert the filter weights by multiplication with a sinusoid,

(1)   \begin{equation*}h_{HPF}[n] = h_{LPF}[n] \cdot cos(\phi n).\end{equation*}

To make the LPF into a HPF it must be upconverted with a center frequency of f_s/2, or in radians \phi = \pi, therefore

(2)   \begin{equation*}cos(\pi n) = (-1)^n,\end{equation*}

(3)   \begin{equation*}h_{HPF}[n] = h_{LPF}[n] \cdot (-1)^n.\end{equation*}

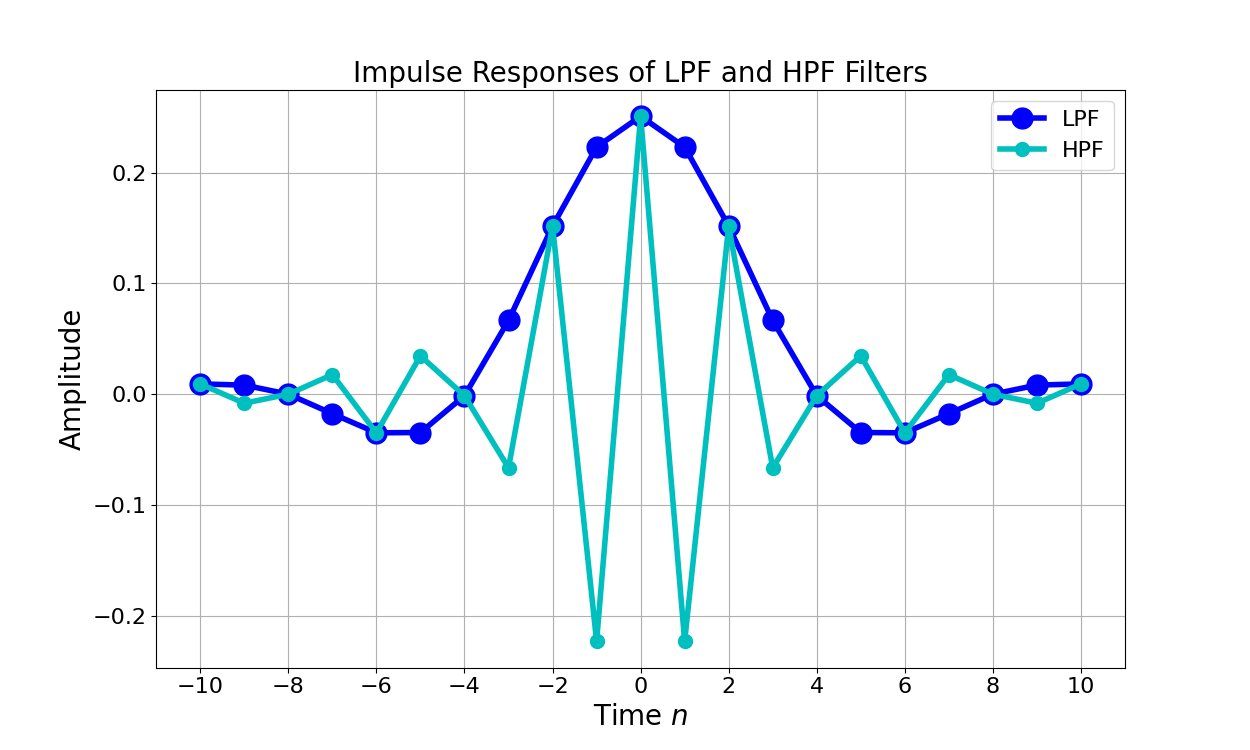
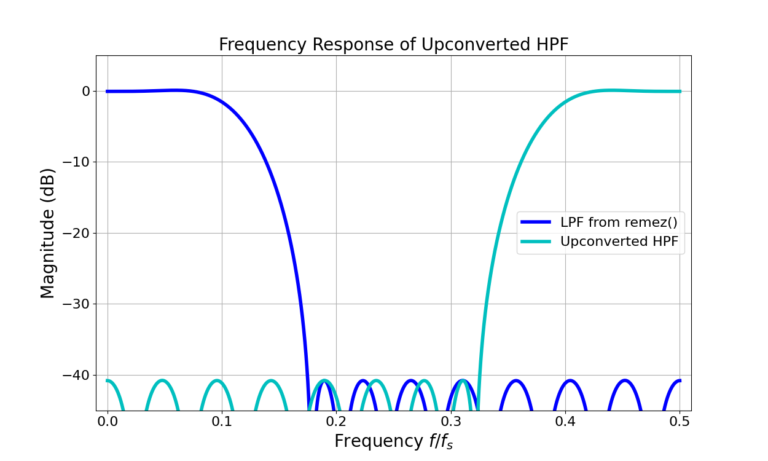
Figure 4 gives the impulse response for an LPF and the upconverted HPF.

Figure 4: The impulse responses of the LPF and HPF filters.
Figure 4: The impulse responses of the LPF and HPF filters.

Frequency Domain Analysis of LPF Upconversion to HPF

The discrete-time Fourier transform of (1) is the frequency-domain convolution of the filter weights h_{LPF}[n] and \cos(\phi n),

(4)   \begin{equation*}\begin{split}H_{HPF}\left(e^{j\omega}\right) & = \mathcal{F} \{ h_{LPF}[n] \cdot cos(\phi n) \} \\& = \mathcal{F} \{ h_{LFP}[n]] \} \ast \mathcal{F} \{ cos(\phi n) \}, \\& = H_{LPF}\left(e^{j\omega}\right) \ast \mathcal{F} \{ cos(\phi n) \},\end{split}\end{equation*}

where \ast is convolution. From (2), conveniently

(5)   \begin{equation*}cos(\pi n) = (-1)^n = e^{j\pi n}.\end{equation*}

The discrete-time Fourier transform of a sequence h[n] multiplied by a complex exponential is [oppenheim1999, p.59]

(6)   \begin{equation*}\mathcal{F} \{ h[n] \cdot e^{j\phi n} \} = H\left( e^{j(\omega - \phi)} \right).\end{equation*}

Substituting \phi = \pi, the Fourier transform (4) can then be written

(7)   \begin{equation*}H_{HPF}\left(e^{j\omega}\right) = H_{LPF}\left(e^{j(\omega-\pi)}\right).\end{equation*}

which is the low-pass filter response frequency shifted to f_s/2 or \pi radians. Figure 5 gives the magnitude of the frequency response in (7) and Figure 6 shows the Remez-designed HPF magnitude frequency response is identical to that of the upconverted HPF.

Figure 5: The magnitudes of the frequency responses for the LPF and upconverted HPF filters.
Figure 5: The magnitudes of the frequency responses for the LPF and upconverted HPF filters.
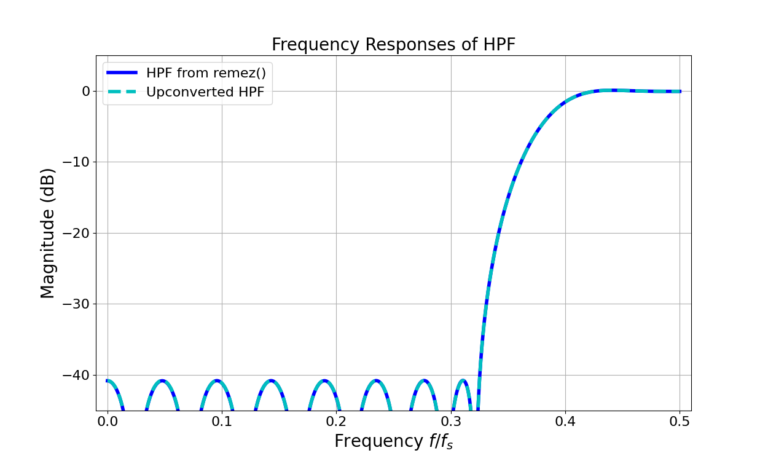
Figure 6: The magnitudes of the frequency responses for the Remez-designed HPF and upconverted HPF are identical.
Figure 6: The magnitudes of the frequency responses for the Remez-designed HPF and upconverted HPF are identical.

Conclusion

A HPF can be designed directly using the remez() function by passing in the appropriate frequency vector and amplitude vector. Alternatively an LPF can be designed and then upconverted to become a HPF through with

(8)   \begin{equation*}h_{HFP}[n] = h_{LPF}[n] \cdot cos(\pi n) = h_{LPF}[n] \cdot (-1)^n.\end{equation*}

Have you seen these blogs on filter design?

Leave a Reply

God, the Lord, is my strength; he makes my feet like the deer’s; he makes me tread on my high places. Habakkuk 3:19

This website participates in the Amazon Associates program. As an Amazon Associate I earn from qualifying purchases.

© 2021-2023 Wave Walker DSP