Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Folding a Polyphase Half Band Filter: Lemon Squeezer Style

October 6, 2021

Introduction

Folding a filter is a way to improve efficiency, and folding the weights for a polyphase filterbank improves the efficiency beyond that. The zero weights in the half band filter make for a great application of the folding and polyphase filterbank structures.

You know after you cut a lemon and try to get the juice out by hand you get to the point where you need a lemon squeezer to get every last drop? This blog is going to squeeze out every little bit of efficiency in the polyphase half band filter.

The half band filter (HBF) was introduced in this blog post and transformed into a decimation by 2 polyphase filter bank (PFB) to reduce the multiplies and improve the efficiency by a factor of 2. This blog will continue by further improving the efficiency to a factor of 8 (not a typo!) by ignoring the zero weight multiples as well as folding the even-symmetric weights to reduce redundant multiplies.

Check out the other posts on half band filters:

Ignoring Zero Half Band Filter Weights

As discussed in this blog post about half the weights in the HBF are zero which contribute nothing to the filter output and should be ignored. An odd-length N half band filter was partitioned into branches $h_{A}[n]$ and $h_{b}[n]$ , an example given in Figure 1.

The branch $h_{B}[n]$ is mostly zeros except for time index

(1) $\begin{equation*}M = \frac{N-1}{4} + \frac{1}{2}\end{equation*}$

and therefore can be simplified as

(2) $\begin{equation*}h_{B}[M] \neq 0,\end{equation*}$

(3) $\begin{equation*}h_{B}[n] = 0 ~ \text{for} ~ n \neq M.\end{equation*}$

The impulse response can be simplified to

(4) $\begin{equation*}z^{-M} \cdot h_{B}[M]\end{equation*}$

which is just a delayed single weight as shown in Figure 2.

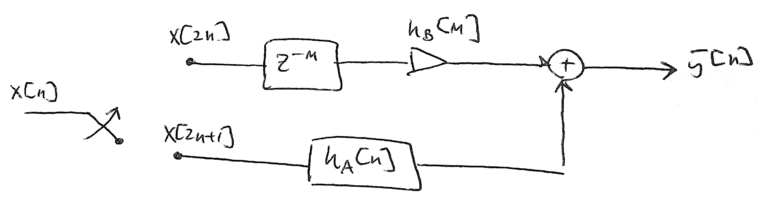
The filter structure from Figure 2 is implemented in the following code:

import numpy as np

# you have to zero pad on the front to account for time-reversal in convolution!
HBFWeightsPad = np.concatenate((np.zeros(1),HBFWeights))

# downsample the input
xA = x[0::2]
xB = x[1::2]

# polyphase partition of HBF
#
# the even indexing starts at one because the HBFWeights were
# zero-padded by 1 sample!
AIndices = np.arange(1,len(HBFWeightsPad),2)
AWeights = HBFWeightsPad[AIndices]

# the odd indexing starts at zero because the HBFWeights were
# zero-padded by 1 sample!
BIndices = np.arange(0,len(HBFWeightsPad),2)
BWeights = HBFWeightsPad[BIndices]

# select the non-zero weight
M = int((filterLength-1)/4 + (1/2))
hB = BWeights[M]

# implement the PFB with ignored zero weights
AOutput = np.convolve(AWeights,xA)
BOutput = np.concatenate((np.zeros(M),hB*xB,np.zeros(M-1)))

# perform summation
yPolyParallel = AOutput + BOutput

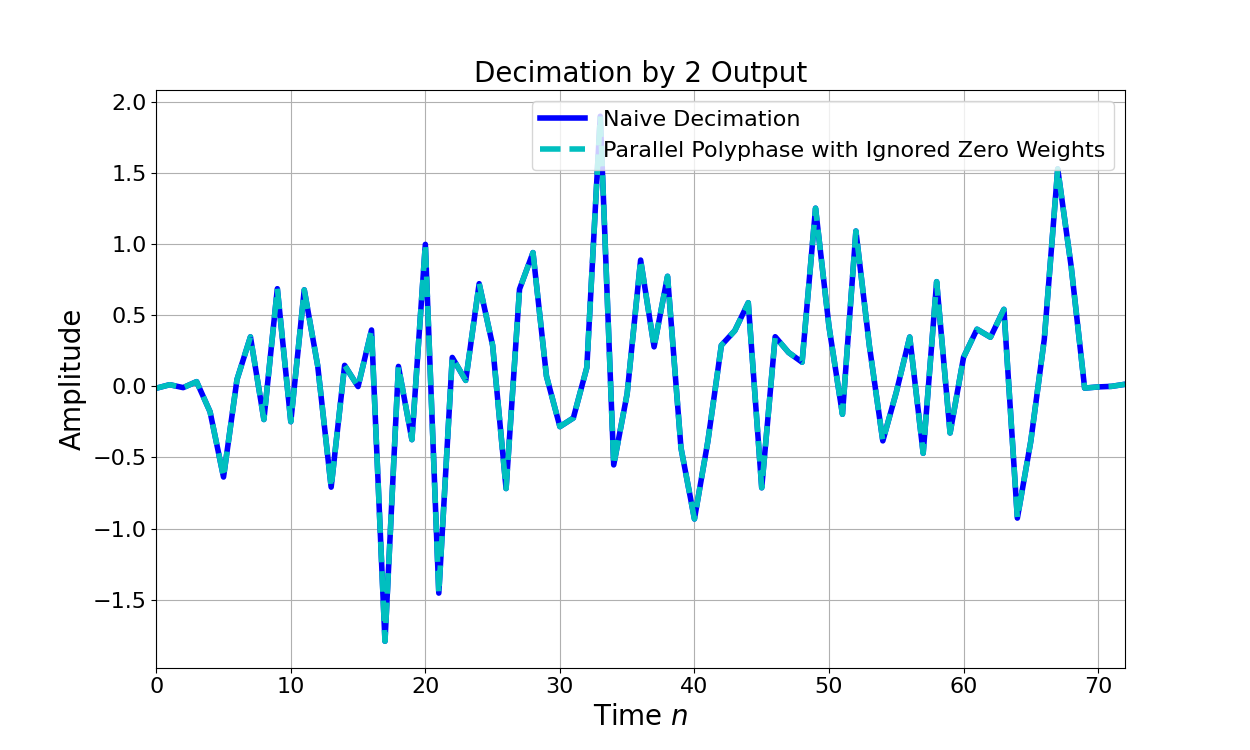
Figure 3 compares the PFB implementation of Figure 2 against the naive implementation of filtering then downsampling showing that the more efficient PBF approach produces the same exact output.

Folded Polyphase Half Band Filter

As shown previously the weights of $h_{A}[n]$ are even-symmetric such that

(5) $\begin{equation*}h_{A}[n] = h_{A}\left[\frac{N-1}{2}-n\right]\end{equation*}$

for $0 \le n \le (N-1)/2$ . Therefore the filter weights for the branch represented by $h_{A}[n]$ can be folded to remove redundant multiplications [lyons2011, p.493, p.702] as shown in Figure 4.

Folding the even-symmetric filter weights reduces the number of multiplications by performing an extra addition of the data beforehand. As an example, without folding the filter branch $h_{A}[n]$ would be implemented as

(6) $\begin{equation*}x[2n+1]h_{A}[0] ~+~ x[2n+3]h_{A}[1] ~+~ x[2n+5]h_{A}[2] ~+~ x[2n+7]h_{A}[3] ~+~ x[2n+9]h_{A}[4] ~+~ x[2n+11]h_{A}[5]\end{equation*}$

which multiplies each input sample in the delay line with the corresponding filter weight. In this example $h_{A}[0] = h_{A}[5]$ , $h_{A}[1] = h_{A}[4]$ and $h_{A}[2] = h_{A}[3]$ . Folding and performing a pre-addition reduces the implementation to

(7) $\begin{equation*}\Big( (x[2n+1] + x[2n+11]) \cdot h_{A}[0] \Big) + \Big( (x[2n+3] + x[2n+9]) \cdot h_{A}[1] \Big) + \Big( (x[2n+5] + x[2n+7]) \cdot h_{A}[2] \Big).\end{equation*}$

The code to implement the folded PFB in Figure 4 is given below:

## implement folded branch for hA[n] # start with zeroed delay line delayLine = np.zeros(len(AWeights))

# zero-pad the input so all input samples to the sample # buffer are filtered xAPad = np.concatenate((xA,np.zeros(len(AWeights)-1)))

# pre-allocate output foldedAOutput = np.zeros(len(xAPad))

for index in range(len(xAPad)):

# add in new sample to delay line delayLine = np.insert(delayLine,0,xAPad[index])

# remove the last sample from the delay line delayLine = delayLine[0:-1]

# perform the pre-add preAdd = delayLine[0:M] + delayLine[-1:-M-1:-1]

# multiply weights weightedPreAdd = preAdd*AWeights[0:M]

# summation foldedAOutput[index] = np.sum(weightedPreAdd)

# folded PFB output yPolyParallelFolded = foldedAOutput + BOutput

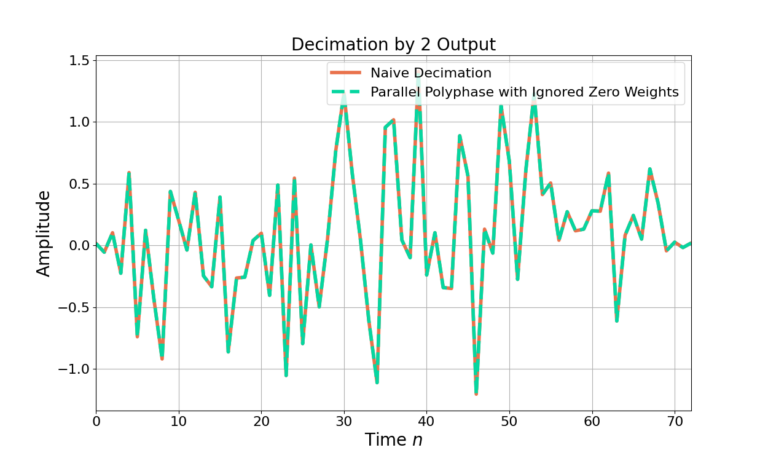
Figure 5 gives an example of the output from the folded PFB with ignored zero weights showing it is the same output as the naive decimation approach.

Computational Efficiency

It was shown prior that applying a PFB structure to a decimate by 2 for filter length N can reduce the amount of multiplies by 1/2. The efficiencies from ignoring the zero weights in $h_{B}[n]$ as well as folding the even-symmetric weights in $h_{A}[n]$ will further reduce the number of multiplies needed to implement the filtering.

Ignoring the zero weights in $h_{B}[n]$ leads to a single multiply for in the branch where there are $(N-1)/2$ multiples in the $h_{A}[n]$ branch in Figure 2. The number of multiplies per output sample is therefore

(8) $\begin{equation*}(N-1)/2 + 1 \approx N/2.\end{equation*}$

As the decimation by 2 PFB structure has already been applied it therefore only takes

(9) $\begin{equation*}1/2 \cdot N/2 \approx N/4\end{equation*}$

multiplies per each input sample which is 4 times as efficient than the naive implementation! The benefit of the PFB approach is that the filtering can be done at the decimated output sample rate as seen here.

For example a half band filter with length N=19 the subfilter corresponding to $h_{B}[n]$ can be implemented with a single multiply and $h_{A}[n]$ implemented with $(N-1)/2 = 9$ for a total of 10 multiples per output sample. However due to the PFB structure the number of multiplies per input sample is 10/2 = 5.

Additional savings come from folding the even-symmetric weights in $h_{A}[n]$ . The filter branch $h_{A}[n]$ has $(N-1)/2 + 1$ weights however half of them are even-symmetric and the number of multiplies can be reduced through a pre-add as in Figure 4. The number of multiplies for an output sample for the $h_{A}[n]$ branch is therefore

(10) $\begin{equation*}(N-1)/4 + 1/2.\end{equation*}$

Adding one multiply for the $h_{B}[n]$ branch to (10), the total number of multiplies per output sample for a half band folded PFB with ignored zero weights is therefore

(11) $\begin{equation*}\frac{N-1}{4} + 1.5 \approx \frac{N}{4}.\end{equation*}$

For example a filter of length N=19 the filter is implemented with $(19-1)/4 + 1.5 = 6$ multiplies.

However the PFB structure allows the filter to run at the output sample rate which is 1/2 the input sample rate, therefore the number of multiples per input sample is

(12) $\begin{equation*}\frac{N}{8}\end{equation*}$

which is 8 times more efficient than the naive decimator!

Improving the efficiency by a factor of 8 is a huge savings! In dB that is $10\text{log}_{10}(8) = 9$ dB. It’s not everyday you find a free 9 dB worth of efficiency to be gained in your system through rearranging some delays, multiplies and adds.

Conclusion

The efficiencies of the polyphase half band filter can be further improved by ignoring zero weights and folding redundant weights. Incorporating the filter structure in Figure 4 makes the implementation 8 times more efficient than the naive decimation approach. Half band filtering then decimating by 2 is useful in real to complex conversion and in large sample rate change through stages, both of which require efficiency since they are often dealing with the largest sample rates within a system.

I think I’ve demonstrated how to get all inefficiencies out of the HBF. If you have a way to further improve the filter structure please email me!

Have you seen the other posts on the half band filter?

2 Responses

Joseph says:

October 13, 2021 at 6:45 pm

The Homer reference was chefs kiss ?

Reply
1. WaveWalkerDSP says:
  
  October 19, 2021 at 10:30 am
  
  I knew you would like it!
  
  You can check out Joe Gaeddert’s work at https://liquidsdr.org and get his Liquid DSP software on github at https://github.com/jgaeddert/liquid-dsp
  
  Reply