Table of Contents
Introduction
You know how on car commercials sometimes it looks like the wheel is spinning backwards? How weird is that? The effect is called aliasing and it occurs when the wheel’s rotation rate is faster than twice the frame rate of the video camera. You can watch a video below that demonstrates aliasing on car tires as well as a video where it appears that a helicopter’s blades have stopped spinning due to a similar effect.
Aliasing is a form of distortion and your DSP systems can be effected by it if not designed appropriately. It might be worth while reviewing the post on frequency and negative frequency before continuing onto the the body of this post.
More blog posts on complex sinusoids:
Aliasing in Sinusoids
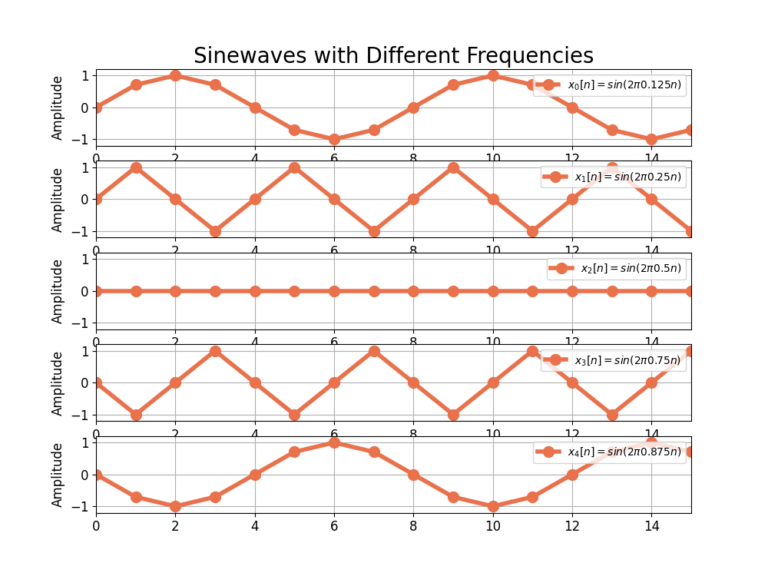
A strange effect happens when ![]() as larger frequencies appears as smaller frequencies. Compare
as larger frequencies appears as smaller frequencies. Compare ![]() against
against ![]() in Figure 1. Both sinusoids appear to have the same frequency of
in Figure 1. Both sinusoids appear to have the same frequency of ![]() but are 180 degrees out of phase. The larger frequency sinusoid can be represented with a negative frequency
but are 180 degrees out of phase. The larger frequency sinusoid can be represented with a negative frequency ![]() ,
,
(2) ![]()
Similarly ![]() looks to have the same frequency as
looks to have the same frequency as ![]() ,
, ![]() , and they are also 180 degrees out of phase. The larger frequency sinusoid can be represented with a negative frequency
, and they are also 180 degrees out of phase. The larger frequency sinusoid can be represented with a negative frequency ![]() ,
,
(3) ![]()
Finally, and maybe weirdest of all, ![]() for all n.
for all n.
If you’ve seen this effect before you’ll know it’s due to aliasing as a result of the Nyquist sampling theorem. Before jumping into that let’s take a look at aliasing in the context of the unit circle.
Aliasing on the Unit Circle
Where Figure 1 only plotted the imaginary portion of a complex sinusoid in the time domain as in (1),
(4) ![]()
Figure 2 to Figure 6 display both the real and imaginary parts of the complex sinusoid on the unit circle where the complex sinusoids are given by
(5) ![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}x_{0}[n] & = e^{j2\pi 0.125 n}, \\x_{1}[n] & = e^{j2\pi 0.25 n}, \\x_{2}[n] & = e^{j2\pi 0.5 n}, \\x_{3}[n] & = e^{j2\pi 0.75 n}, \\x_{4}[n] & = e^{j2\pi 0.875 n}. \\\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-8cf9eb3e6c6f7da2669974df1cb30c82_l3.png)
Figure 2 shows the complex sinusoid ![]() for n=0 to n=7. The angle of the complex sinusoid
for n=0 to n=7. The angle of the complex sinusoid ![]() is plotted in red and shows the instantaneous phase on
is plotted in red and shows the instantaneous phase on ![]() . The angle shows a perceived rotation in the counter-clockwise direction which is a positive frequency. The complex sinusoid takes 8 samples to go one full rotation around the unit circle therefore the perceived frequency is
. The angle shows a perceived rotation in the counter-clockwise direction which is a positive frequency. The complex sinusoid takes 8 samples to go one full rotation around the unit circle therefore the perceived frequency is ![]() .
.
![Figure 2: The complex sinusoid x0[n] = e(j2 pi 0.125 n) plotted in the complex plane.](https://www.wavewalkerdsp.com/wp-content/uploads/2021/10/aliasingSamplingCarTires_sinusoidsUnitCircleGrid0.png)
Figure 3 shows the complex sinusoid ![]() for n=0 to n=7. The angle shows a positive frequency the complex vector appears to be rotating in the counter-clockwise direction. The complex sinusoid takes 4 samples to go one full rotation around the unit circle therefore the perceived frequency is
for n=0 to n=7. The angle shows a positive frequency the complex vector appears to be rotating in the counter-clockwise direction. The complex sinusoid takes 4 samples to go one full rotation around the unit circle therefore the perceived frequency is ![]() .
.
![Figure 3: The complex sinusoid x1[n] = e(j2 pi 0.25 n) plotted in the complex plane.](https://www.wavewalkerdsp.com/wp-content/uploads/2021/10/aliasingSamplingCarTires_sinusoidsUnitCircleGrid1.png)
Figure 4 shows the complex sinusoid ![]() for n=0 to n=7. The angle is a special case in that it alternates between 0 and
for n=0 to n=7. The angle is a special case in that it alternates between 0 and ![]() which can be considered rotation in the clockwise direction or counter-clockwise direction. The complex sinusoid takes 2 samples to go one full rotation around the unit circle therefore the perceived frequency is
which can be considered rotation in the clockwise direction or counter-clockwise direction. The complex sinusoid takes 2 samples to go one full rotation around the unit circle therefore the perceived frequency is ![]() .
.
![Figure 4: The complex sinusoid x2[n] = e(j2 pi 0.5 n) plotted in the complex plane.](https://www.wavewalkerdsp.com/wp-content/uploads/2021/11/aliasingSamplingCarTires_sinusoidsUnitCircleGrid2.png)
Figure 5 shows the complex sinusoid ![]() for n=0 to n=7. The angle is rotating in a clockwise direction and the complex sinusoid takes 4 samples to go one full rotation around the unit circle therefore the perceived frequency is
for n=0 to n=7. The angle is rotating in a clockwise direction and the complex sinusoid takes 4 samples to go one full rotation around the unit circle therefore the perceived frequency is ![]() although in reality it is
although in reality it is ![]() . The aliased frequency can be represented by
. The aliased frequency can be represented by ![]() radians which is the perceived frequency seen in Figure 5. The complex vector appearing to rotate in the opposite direction is the exact same effect as the car tire rotating in the opposite direction as in the YouTube video above.
radians which is the perceived frequency seen in Figure 5. The complex vector appearing to rotate in the opposite direction is the exact same effect as the car tire rotating in the opposite direction as in the YouTube video above.
![Figure 5: The complex sinusoid x3[n] = e(j2 pi 0.75 n) plotted in the complex plane.](https://www.wavewalkerdsp.com/wp-content/uploads/2021/10/aliasingSamplingCarTires_sinusoidsUnitCircleGrid3.png)
Figure 6 shows the complex sinusoid ![]() for n=0 to n=7. The angle is rotating in a clockwise direction and the complex sinusoid takes 8 samples to go one full rotation around the unit circle therefore the perceived frequency is
for n=0 to n=7. The angle is rotating in a clockwise direction and the complex sinusoid takes 8 samples to go one full rotation around the unit circle therefore the perceived frequency is ![]() although in reality it is
although in reality it is ![]() . The aliased frequency can be represented by
. The aliased frequency can be represented by ![]() radians which is the perceived frequency seen in Figure 6. The complex vector seemingly rotating in a clockwise direction rather than the counter-clockwise direction is the exact same effect as the car tire appearing to rotate in the reverse direction as in the YouTube video above.
radians which is the perceived frequency seen in Figure 6. The complex vector seemingly rotating in a clockwise direction rather than the counter-clockwise direction is the exact same effect as the car tire appearing to rotate in the reverse direction as in the YouTube video above.
![Figure 6: The complex sinusoid x4[n] = e(j2 pi 0.875 n) plotted in the complex plane.](https://www.wavewalkerdsp.com/wp-content/uploads/2021/10/aliasingSamplingCarTires_sinusoidsUnitCircleGrid4.png)
Nyquist Sampling Theorem
When ![]() the actual frequency matches the perceived frequency, as in Figure 2 and Figure 3, and the complex sinusoid rotates around the unit circle in a counter-clockwise direction. Figure 4 shows an interesting phenomenon: the direction of the rotation around the unit circle cannot be stated to be either clockwise or counter-clockwise when
the actual frequency matches the perceived frequency, as in Figure 2 and Figure 3, and the complex sinusoid rotates around the unit circle in a counter-clockwise direction. Figure 4 shows an interesting phenomenon: the direction of the rotation around the unit circle cannot be stated to be either clockwise or counter-clockwise when ![]() . When
. When
(6) ![]()
the perceived frequency appears to be negative ![]() and the complex vector is rotating in a clockwise direction.
and the complex vector is rotating in a clockwise direction.
The Nyquist sampling theorem states that a signal can be perfectly reconstructed if it is sampled with frequency ![]() which is greater than or equal to twice the largest frequency
which is greater than or equal to twice the largest frequency ![]() in the signal [Proakis2007, p.13]
in the signal [Proakis2007, p.13]
(7) ![]()
Another way to state the Nuyquist sampling theorem is that no aliasing distortion will occur if the ratio of the largest frequency ![]() in the signal to sampling frequency
in the signal to sampling frequency ![]() is less than or equal to 1/2,
is less than or equal to 1/2,
(8) ![]()
Note that the ratio in (8) is the boundary upon which aliasing occurs which can be seen in Figure 1 through Figure 6. When ![]() the actual frequency and perceived frequency are the same, however when
the actual frequency and perceived frequency are the same, however when ![]() the frequency is aliased or “folded” to frequency
the frequency is aliased or “folded” to frequency ![]() [Lyons2011, p.40].
[Lyons2011, p.40].
Conclusion
Aliasing is a form of distortion and occurs when the Nyquist sampling rate ![]() is not satisfied. Aliasing causes actual frequencies
is not satisfied. Aliasing causes actual frequencies ![]() to be folded into negative frequencies
to be folded into negative frequencies ![]() causing distortion of the underlying signal. Maintaining the proper ratio of sample rate to signal bandwidth in each operation in your DSP system will avoid aliasing.
causing distortion of the underlying signal. Maintaining the proper ratio of sample rate to signal bandwidth in each operation in your DSP system will avoid aliasing.
More blog posts on complex sinusoids:
![Figure 3: The complex sinusoid e(j2 pi (2/4) n) only contains energy at X[2].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/8136-featured-125x100.png)







