Table of Contents
Introduction
Sooner or later you’re going to have to apply a derivative to a discrete-time signal. An example would be building a derivative matched filter (DMF) for timing recovery [harris2021, p.490]. This brings us to our first piece of DSP Wisdom: If you need to do something in DSP it’s best to do it with a filter. So how do you build a derivative filter?
We’ll start with the derivation in continuous-time to make the math tractable then transform it into discrete-time. A follow-up post will discuss methods and alternatives for designing the derivative filter weights. Richard Lyons has a really great section on derivative filters in his textbook that is totally worth your time if you’re interested in more information on the topic [lyons2011, p.361].
Check out these other posts on filter design:
Continuous-Time Derivative Filter
The time-derivative of signal ![]() can be written as the derivative of the inverse Fourier transform,
can be written as the derivative of the inverse Fourier transform,
(1) ![]()
Pulling the derivative ![]() through the integral in (1) results in
through the integral in (1) results in
(2) ![]()
The derivative of the complex sinusoid can be written as
(3) ![]()
Substituting the derivative (3) into (2) can be written as
(4) ![]()
The signal derivative (4) can be rewritten using the inverse Fourier transform operator ![]() such that
such that
(5) ![]()
A frequency-domain derivative filter is defined as
(6) ![]()
such that (5) is
(7) ![]()
The product of two frequency-responses A(f) and B(f) are related through the Fourier transform to the convolution ![]() of their impulse-responses a(t) and b(t)
of their impulse-responses a(t) and b(t)
(8) ![]()
The signal derivative (7) can therefore be written as the convolution of two impulse-responses, the signal x(t) and the derivative filter h(t),
(9) ![]()
The impulse response of the derivative filter is defined through the inverse Fourier transform
(10) 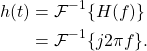
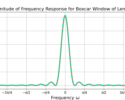
Figure 1 is a 3D plot of the frequency-response H(f) for some values of f where
(11) ![]()
(12) ![]()
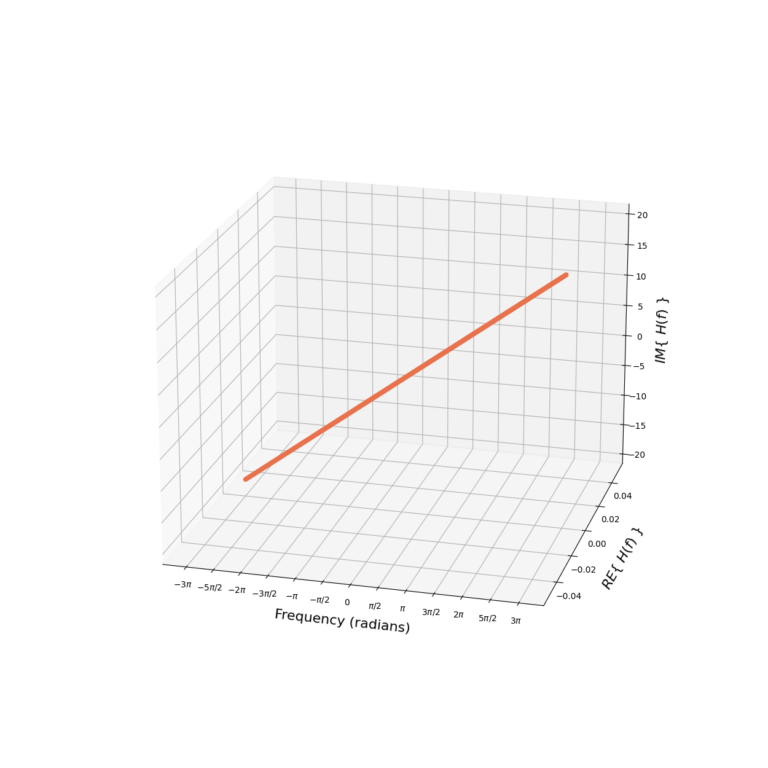
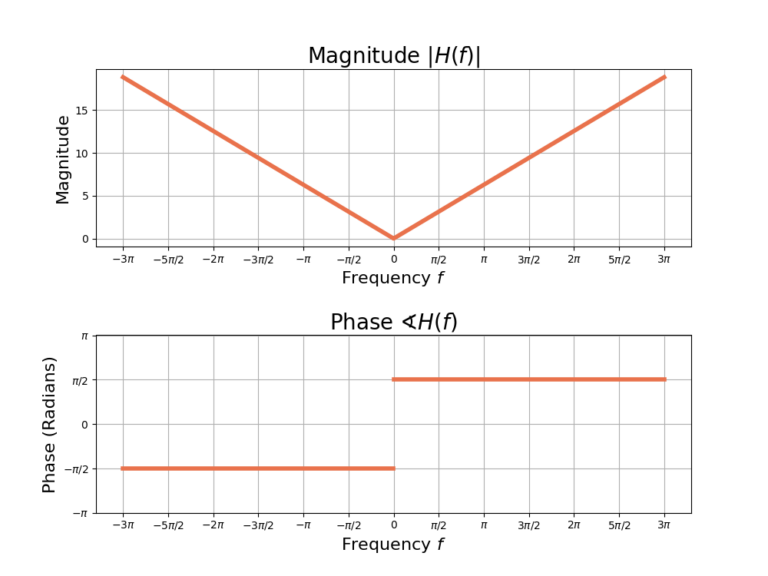
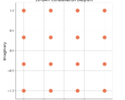
The magnitude ![]() and phase
and phase ![]() of the derivative filter are given in Figure 2.
of the derivative filter are given in Figure 2.
Transforming into a Discrete-Time Frequency Response
A discrete-time implementation of ![]() from (6) is created by truncating the frequency response. Where H(f) is defined over
from (6) is created by truncating the frequency response. Where H(f) is defined over ![]() the discrete-time Fourier transform (DTFT) is defined by
the discrete-time Fourier transform (DTFT) is defined by
(13) ![]()
where
(14) ![]()
The sampling rate defines the amount of truncation such that ![]() is defined over
is defined over ![]() or equivalently
or equivalently ![]() .
.
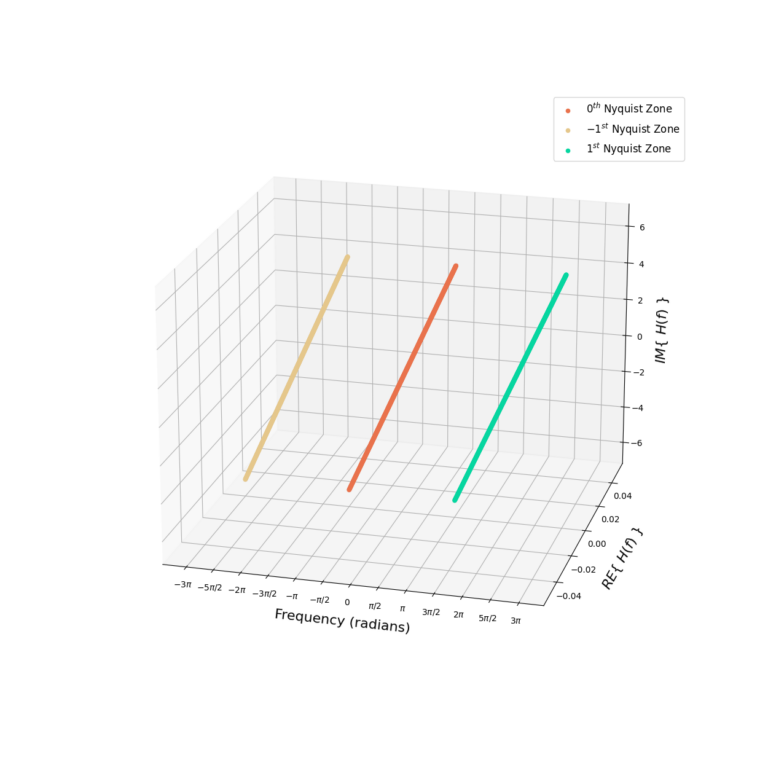
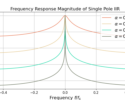
Figure 3 gives the frequency-response ![]() for the discrete-time derivative filter. The frequency-response is periodic in
for the discrete-time derivative filter. The frequency-response is periodic in ![]() and three repetitions are shown, denoted as Nyquist zones -1, 0 and 1. Figure 4 is the magnitude
and three repetitions are shown, denoted as Nyquist zones -1, 0 and 1. Figure 4 is the magnitude ![]() and phase
and phase ![]() which also shows three Nyquist zones.
which also shows three Nyquist zones.
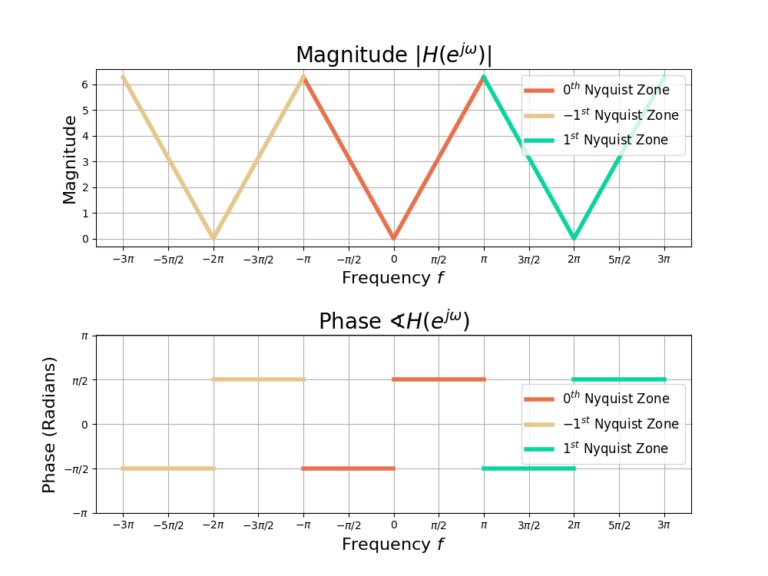
Discrete-Time Derivative Filter
The continuous-time frequency-response H(f) in (6) was mapped into discrete-time ![]() in (13). The inverse DTFT is used to transform
in (13). The inverse DTFT is used to transform ![]() into the impulse-response h[n] where the inverse DTFT is given by [oppenheim1999, p.48]
into the impulse-response h[n] where the inverse DTFT is given by [oppenheim1999, p.48]
(15) ![]()
Substituting ![]() from (13) into (15) results in
from (13) into (15) results in
(16) ![]()
The inverse DTFT integral (16) can be solved through the use of integration by parts. Define u and v according to
(17) 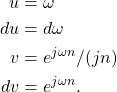
Integration by parts of the inverse DTFT integral (16) is defined as
(18) ![]()
and substituting (17) into (18) results in
(19) ![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}h[n] & = \frac{j}{2\pi} \left( \frac{\omega}{jn} e^{j\omega n} \Big|_{-\pi}^{\pi} - \int_{-\pi}^{\pi} \frac{1}{jn} e^{j\omega n} d\omega \right) \\& = \frac{\omega}{2\pi n} e^{j\omega n} \Big|_{-\pi}^{\pi} - \frac{1}{2\pi n} \int_{-\pi}^{\pi} e^{j\omega n} d\omega. \end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-f441b20376c715d4ac6ce355ec512298_l3.png)
Evaluating the Integral (Part 1)
The first part of (19) can be simplified as
(20) 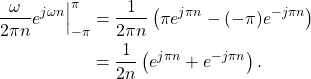
Equation (20) can be simplified to
(21) ![]()
The term ![]() can be written as
can be written as
(22) ![]()
for all n, however evaluating (21) at n=0 must be done through L’Hopital’s rule,
(23) 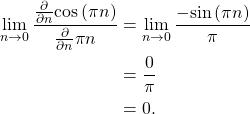
Using (23) and (22), equation (21) is written as
(24) 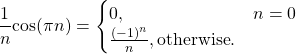
Evaluating The Integral (Part 2)
The second part of (19) is
(25) 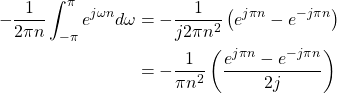
which can be simplified by a trigonometric identity to
(26) ![]()
The term ![]() can be reduced to
can be reduced to
(27) ![]()
for all n, however evaluating (26) at n=0 must be done through L’Hopital’s rule. Applying L’Hopital’s Rule on (26) is
(28) 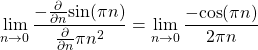
which still cannot be evaluated at n=0 and therefore the rule is applied once more,
(29) 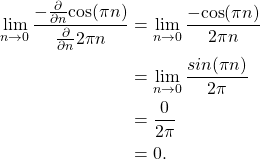
Derivative Filter Impulse Response
![Figure 5: Impulse response of the derivative filter h[n] for -32](https://www.wavewalkerdsp.com/wp-content/uploads/2021/11/derivativeFilterDerivation_derivativeFilterImpulseResponse-1-768x576.png)
![Figure 6: Magnitude and phase of the frequency response for F( h[n] ).](https://www.wavewalkerdsp.com/wp-content/uploads/2021/11/derivativeFilterDerivation_derivativeFilterFreqResponse-768x576.png)
Conclusion
A derivative filter is a useful tool to have in your DSP kit. The derivation starts with a time-derivative of the frequency-response which results in the product of two frequency responses, or equivalently the convolution of two impulse-responses. Applying the inverse DTFT results in an infinitely long impulse response for the derivative filter.
Figure 6 shows a different magnitude and phase than the ideal plots in Figure 2. Be on the look out for part 2 in which the differences will be discussed in detail and methods will be given for designing derivative filter weights.
Check out these other posts on filter design:






![Rendered by QuickLaTeX.com \begin{equation*}h[n] = \begin{cases}\frac{(-1)}{n}, & n \neq 0 \\0, & n = 0\end{cases}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-ea8134559d400d57898be8389f5e143a_l3.png)
2 Responses
Oh no! My entire career in DSP contradicts your Wisdom: “If you need to do something in DSP it’s best to do it with a filter.” Here “filter” means “linear time-invariant system,” which means the input and output of the “something” is a convolution, and convolutions are linear. But cyclostationary signal processing, spectrum estimation, frequency translation, and many signal-parameter estimators involve nonlinear operations. We need some more Wisdom to cover those of us working on the fringes of DSP–I agree that linear time-invariant systems are foundational, but what about us poor nonlinear signal processors?? 🙂
Good catch! I’m trying to move people away from just throwing NumPy at a DSP problem without thinking about how it would impact the impulse and frequency responses. I agree that non-linearities are useful in DSP but they need to come with a safety warning.
There’s a lot of goodness to be had just by averaging through filtering, and I put things like CSP and spectral estimation into that general bucket. I’m using “filter” loosely, broader than just LTI systems. Correlation, convolution and FIR filters all feel like they are siblings and that’s what I’m trying to get at when I say “use a filter”.