Table of Contents
Introduction
I came across a question on DSP Stack Exchange the other day: can the Fourier Transform magnitude be negative? This is a great question! The answer is no, and let’s take a look at why.
More blogs on DSP:
Discrete Time Fourier Transform
The discrete-time Fourier transform (DTFT) is
(1) ![]()
The DTFT is a cross correlation of x[n] with a complex exponential ![]() . The summation over all n produces a single complex number. The DTFT is written as a real and imaginary component,
. The summation over all n produces a single complex number. The DTFT is written as a real and imaginary component,
(2) ![]()
where
(3) ![]()
and
(4) ![]()
Magnitude of Complex Number
Rather than use the complex number in (2) a simpler representation is given by
(5) ![]()
where the complex number c has a real part a and an imaginary part jb. The magnitude of a complex number c can be written as
(6) ![]()
The magnitude can be written in terms of a and b by substituting (5) into (6),
(7) 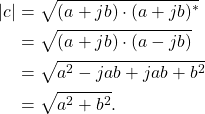
The square of a real number ![]() and
and ![]() cannot be negative and the square root of a positive number is always positive, therefore the magnitude
cannot be negative and the square root of a positive number is always positive, therefore the magnitude ![]() cannot be negative.
cannot be negative.
Plotting Magnitude of Complex Number
Conceptually the magnitude of a complex number c is the length of the vector beginning at the origin 0 + 0j and ending at c. Consider a complex number
(8) ![]()
Figure 1 plots the complex vector c in 2D complex space.
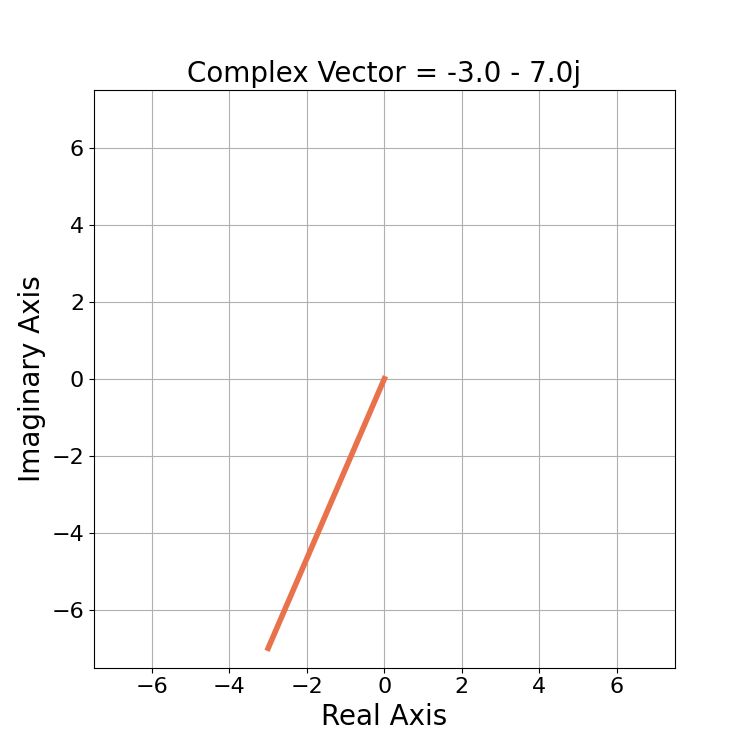
The magnitude ![]() is the distance from 0+0j to -3-7j which is
is the distance from 0+0j to -3-7j which is
(9) 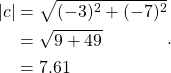
Fourier Transform Magnitude
Using the representation in (2) for the complex number the magnitude can be written as
(10) ![]()
which is always a positive number.
Conclusion
The magnitude of a complex number always has to be positive by definition, it can never be negative. The magnitude is conceptually the length of a complex vector which is written mathematically as ![]() .
.
More blogs on DSP:
Got a question? Drop it in the comments below.








One Response
I definitely agree that the magnitude of the Fourier transform, or any complex number, is non-negative. But students or newcomers to DSP might be a bit confused about this statement: “the square root of a positive number is always positive.” Because square roots of positive numbers can be negative: -2 is a valid square root of 4. I think the difference is in the definition of “magnitude” (or “modulus” or “absolute value”) which is defined as the positive square root.
When we use the square-root symbol, and there is no ‘-‘ or ‘+’ in front of it, ‘+’ is assumed.
Interested readers might look into metric spaces and inner products:
https://en.wikipedia.org/wiki/Magnitude_(mathematics)
https://en.wikipedia.org/wiki/Euclidean_space#Euclidean_norm