Wave Walker DSP

DSP Algorithms for RF Systems

Brand New Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Previous image

Next image

Designing FIR Filter Gain

February 23, 2022

Introduction

This blog describes how to design the FIR filter gain through normalization and then applying a gain. Applying filter gain may be desirable to setting the proper amplitude level or power level needed for follow on processing based on threshold values or other reference levels.

Filter design methods may create different gains for the resulting filters such as with Remez, using windowed sinc functions or as specially designed pulse shaping filters. Normalizing the magnitude response of an FIR filter makes the gain 1, or 0 dB, at a desired frequency. A gain factor can then be applied by scaling each of the filter weights.

More blogs on filter design:

Normalizing FIR Filter Gain

Normalizing a filter to unit gain at some frequency $\omega_g$ is as simple as dividing the filter weights by the magnitude of the discrete-time Fourier transform (DTFT) at $\omega_g$

(1) $\begin{equation*}h_{norm}[n] = \frac{h[n]}{\left|\sum_{k} h[k]e^{-j\omega_g k}\right|}\end{equation*}$

where $h_{norm}[n]$ is the normalized filter and h[n] is the unnormalized filter. To see why this is the case, start by taking the DTFT of h[k] which is

(2) $\begin{equation*}H\left(e^{j\omega}\right) = \sum_{k} h[k]e^{-j\omega k}.\end{equation*}$

The unnormalized filter gain at $\omega_g$ is the magnitude of the frequency response

(3) $\begin{equation*}\left| H\left( e^{j\omega} \right) \right|_{\omega = \omega_g} = \left| \sum_{k} h[k]e^{-j \omega_g k} \right|\end{split}\end{equation*}$

A filter gain of 1 at $\omega_g$ is achieved by scaling the frequency response (2) by the unnormalized filter gain at $\omega_g$ (3). The frequency response of the normalized filter is therefore

(4) $\begin{equation*}\begin{split}H_{norm} \left( e^{j\omega} \right) & = \frac{ H \left( e^{j\omega} \right) }{ \left| H \left( e^{j\omega} \right) \right|_{\omega=\omega_g} } \\& = \frac{ H \left( e^{j\omega} \right) } { \left| \sum_{k} h[k] e^{-j\omega_g k} \right| }.\end{split}\end{equation*}$

The time-domain filter weights are the inverse DTFT of (4)

(5) $\begin{equation*}\mathcal{F}^{-1} \left\{ H_{norm} \left( e^{j\omega} \right) \right\} = \frac{ \mathcal{F}^{-1} \left\{ H \left( e^{j\omega} \right) \right\} }{ \left| \sum_{k} h[k]e^{-j\omega_g k} \right| }\end{equation*}$

which is the same as (1)

(6) $\begin{equation*}h_{norm}[n] = \frac{ h[n] }{ \left| \sum_{k} h[k]e^{-j\omega_g k} \right| }.\end{equation*}$

Scaling FIR Filter Gain

The filter gain in dB is measured by the magnitude-squared when working in the logarithmic domain

(7) $\begin{equation*}10\text{log}_{10} \left( \left| X \left( e^{j\omega} \right) \right|^2 \right) = 20\text{log}_{10} \left( \left| X\left( e^{j\omega} \right) \right| \right).\end{equation*}$

The linear gain G and logarithmic gain $G_{dB}$ are related through

(8) $\begin{equation*}\begin{split}G_{dB} & = 10\text{log}_{10}\left( G^2 \right) \\& = 20\text{log}_{10} \left( G \right)\end{split}\end{equation*}$

or equivalently

(9) $\begin{equation*}\begin{split}G & = 10^{G_{dB}/20}\end{split}\end{equation*}$

where G > 0. The scaled filter weights $h_{g}[n]$ are therefore

(10) $\begin{equation*}\begin{split}h_{g}[n] & = G \cdot h_{norm}[n] \\& = \frac{G \cdot h[n]}{\left| \sum_{k} h[k]e^{-j\omega_{g} k} \right| }.\end{split}\end{equation*}$

Examples for Designing FIR Filter Gain

Low Pass Filter Example

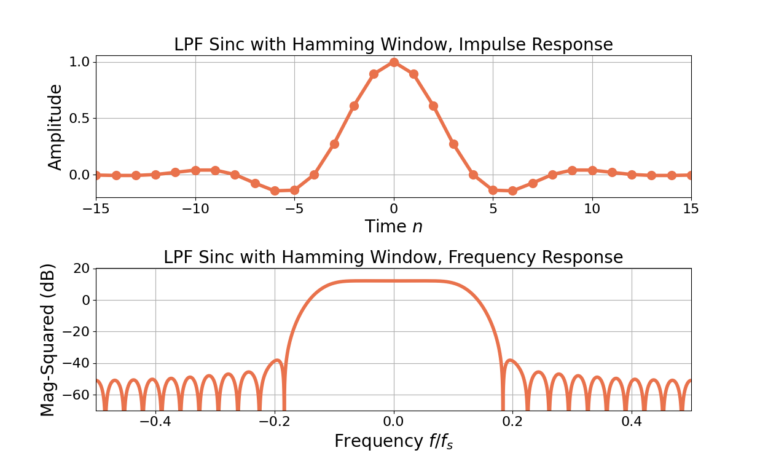
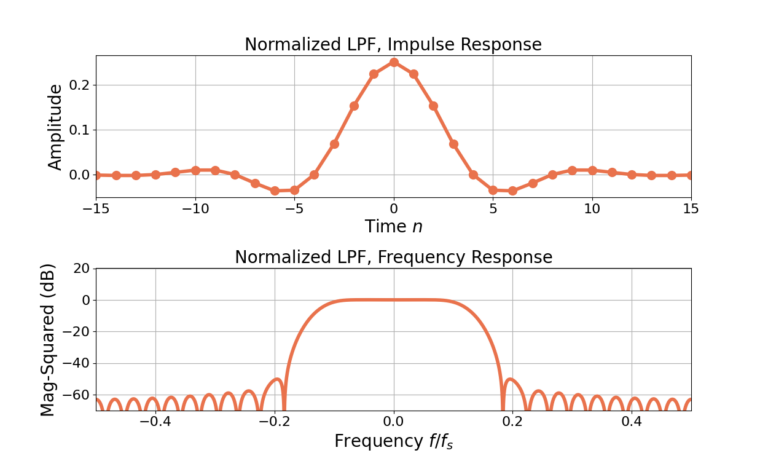
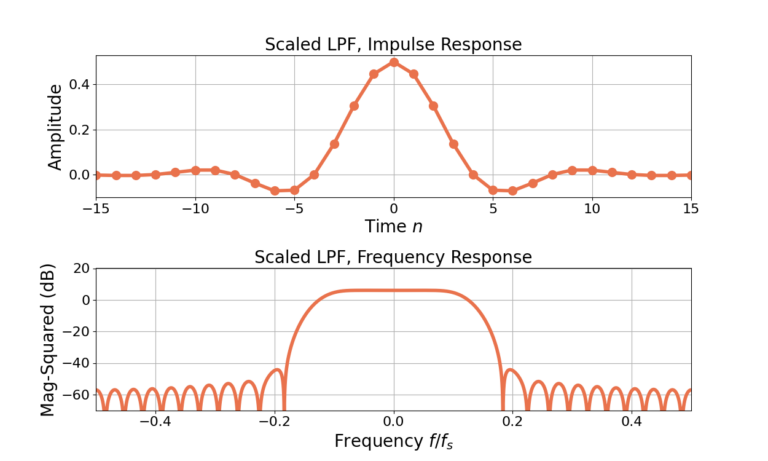
Figure 1 gives the impulse and frequency responses for an unnormalized sinc with 31 filter weights with a Hamming window applied. Figure 2 gives the responses after the filter is normalized to 0 dB gain at $\omega = 0$ using (6) and Figure 3 gives the responses after scaling the same filter to have a gain of 6 dB at $\omega = 0$ using (10).

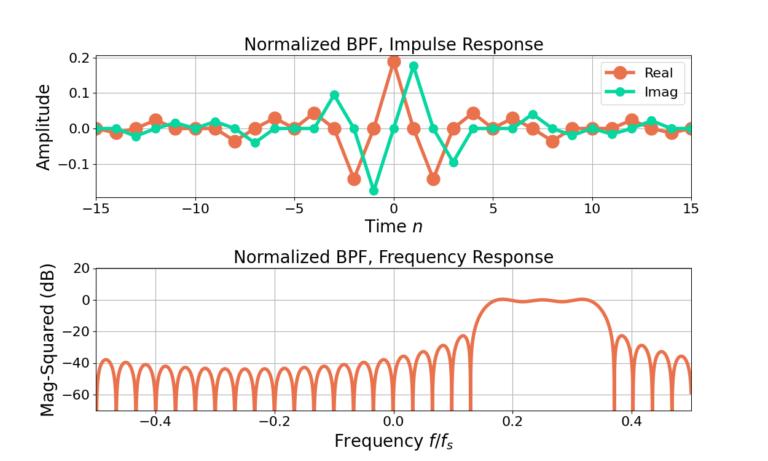
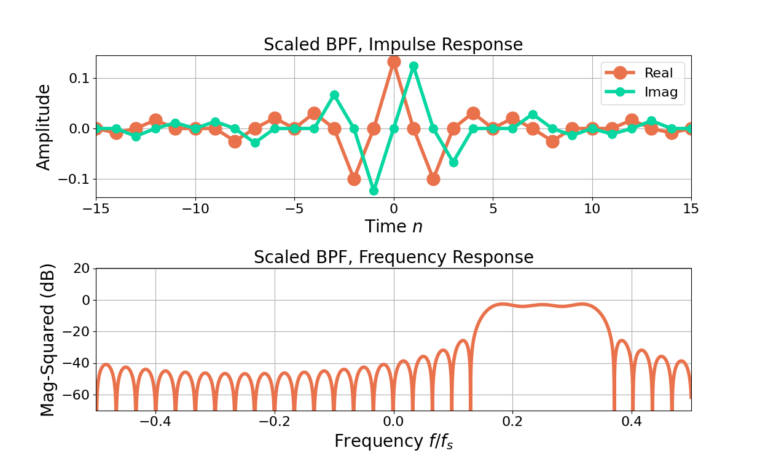
Band Pass Filter Example

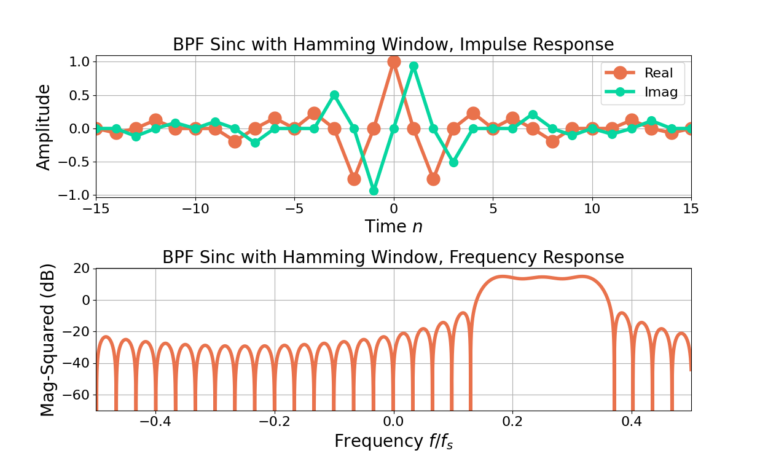
Figure 4 gives the impulse and frequency responses for an unnormalized sinc with 31 filter weights with a Hamming window applied and then frequency shifted to band-pass. Figure 5 gives the responses after the filter is normalized to 0 dB gain at $\omega = \pi/2$ , which is equivalent to $f/f_s = 0.25$ , using (6) and Figure 6 gives the responses after scaling the same filter to have a gain of -3 dB using(10).

Conclusion

The gain of an FIR filter can be designed by first normalizing the weights to unit gain at frequency $\omega_g$ and then scaling each of the weights by the desired linear gain. The filter normalization is calculated by diving the filter weights by the magnitude of the frequency response at $\omega_g$ .

More blogs on filter design:

God, the Lord, is my strength; he makes my feet like the deer’s; he makes me tread on my high places. Habakkuk 3:19