![Figure 1: The two sequences for the autocorrelation of x0[n] and x0[n].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/5515-featured-75x75.png)
Table of Contents
Introduction
Complex frequency shifting moves the frequency response of a signal in the frequency domain. This blog describes complex frequency shifting in continuous time by multiplying a signal with a complex exponential.
More blogs!
Complex Frequency Shifting in the Frequency Domain
Complex frequency shifting is the process of changing the location of a signal in the frequency domain. For a signal 
the frequency response is defined as 
, related through the Fourier transform
(1) 
Complex frequency shifting by frequency 
moves the frequency response within the frequency domain. Mathematically, complex frequency shifting in the frequency domain is represented by substituting
(2) 
such that the frequency response is now
(3) 
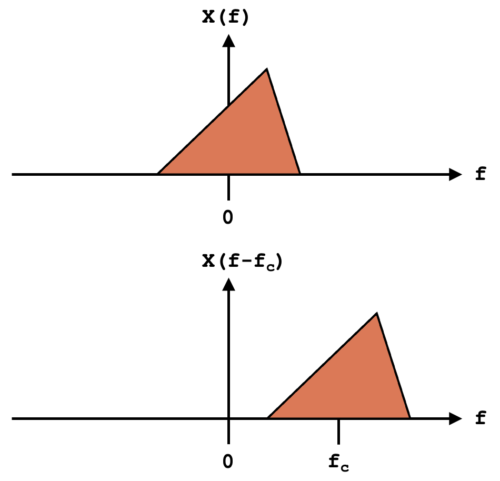
Figure 1 gives an example of how can be frequency shifted by frequency .
Complex Frequency Shifting in the Time Domain
Complex frequency shifting in the time domain is accomplished by multiplying a signal with a complex sinusoid,
(4) 
resulting in
(5) 
The Fourier transform of (5) is defined by (reference)
(6) 
where 
represents linear convolution. The Fourier transform of (4) is defined as (reference)
(7) 
(8) 
which can be simplified as
(9) 
from the Dirac delta sifting theorem (reference).
Conclusion
Multiplication of with 
shifts the frequency response of by resulting in 
.
More blogs!