Table of Contents
Introduction
This blog derives the frequency response of a complex sinusoid using the discrete Fourier transform (DFT). The derivation starts by apply the discrete time Fourier transform (DTFT) of the complex sinusoid, simplifying the summation as a geometric series, and evaluating the DTFT at specific frequencies of the DFT.
Check out these other blogs:
Discrete Time Fourier Transform
The discrete-time Fourier transform (DTFT) is defined as [Oppenheim1999, p.48]
(1) ![]()
A realizable (ex: can be built in the real world) digital system must deal with signals which are finite length. A finite length complex sinusoid is defined according to
(2) ![Rendered by QuickLaTeX.com \begin{equation*}x[n] =\begin{cases}e^{j\omega_c n}, & 0 \le n \le N-1 \\0, & \text{otherwise}.\end{cases}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-4956323410cf548a82ae79f49beaa7bc_l3.png)
(3) 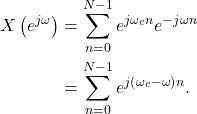
Geometric Series
Applying L'Hospital's Rule
Equation (9) is undefined when ![]() therefore L’Hospital’s rule is applied,
therefore L’Hospital’s rule is applied,
(10) 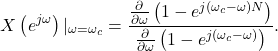
Simplifying (10),
(11) 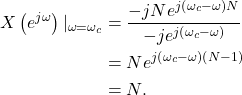
The frequency response can therefore be written as
(12) 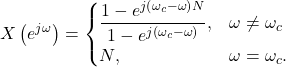
Discrete Fourier Transform (DFT) of Complex Sinusoid
The DFT is a simplified case of the DTFT where the frequencies ![]() are only evaluated at
are only evaluated at
(13) ![]()
where ![]() , [Oppenheim1999, p.542]. Substituting (13) into (12),
, [Oppenheim1999, p.542]. Substituting (13) into (12),
(14) ![Rendered by QuickLaTeX.com \begin{equation*}X[k] = \begin{cases}\dfrac{1-e^{j\left(\omega_c - 2\pi k/N\right)N}}{1-e^{j\left(\omega_c-2\pi k/N\right)}}, & 2\pi k/N \neq \omega_c \\N, & 2\pi k/N = \omega_c.\end{cases}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-9275aab248f56f4aa42251f3c7c13c68_l3.png)
The DFT (14) can be further simplified as
(15) ![Rendered by QuickLaTeX.com \begin{equation*}X[k] = \begin{cases}e^{j\alpha\left(N-1\right)/2}\cdot \dfrac{\sin\left( \alpha N/2 \right)}{\sin \left( \alpha/2 \right)}, & 2\pi k/N \neq \omega_c, \\N, & 2\pi k/N = \omega_c.\end{cases}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-312594a8f5d4d0c353356d3a172e353d_l3.png)
Comparing to Simulation
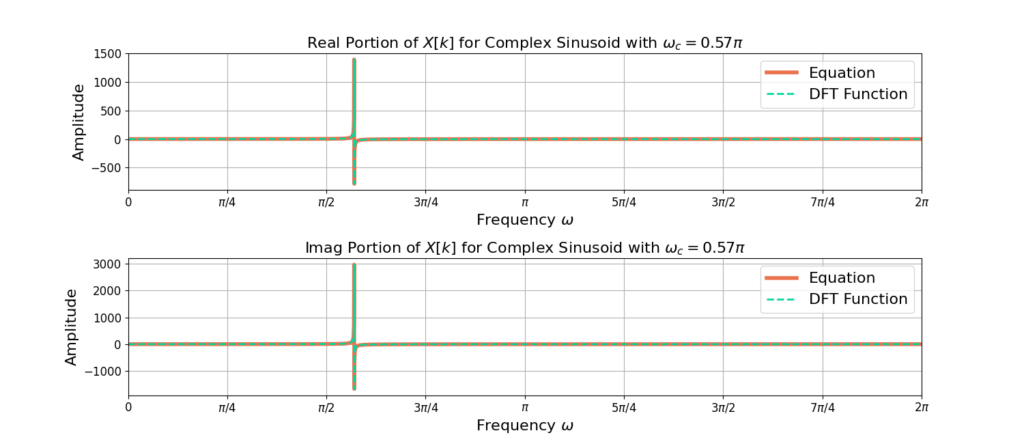
Figures 1-3 compare equation (15) to NumPy’s DFT function for sinusoids with frequencies ![]() and N=4096.
and N=4096.
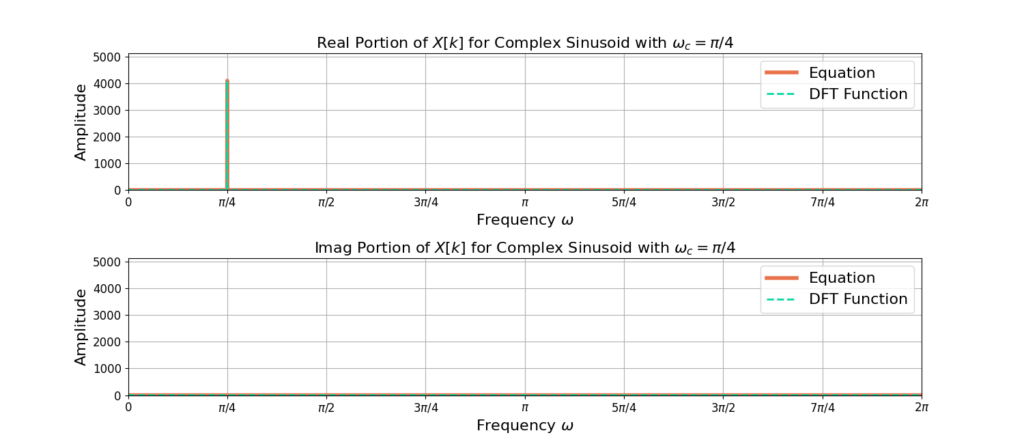
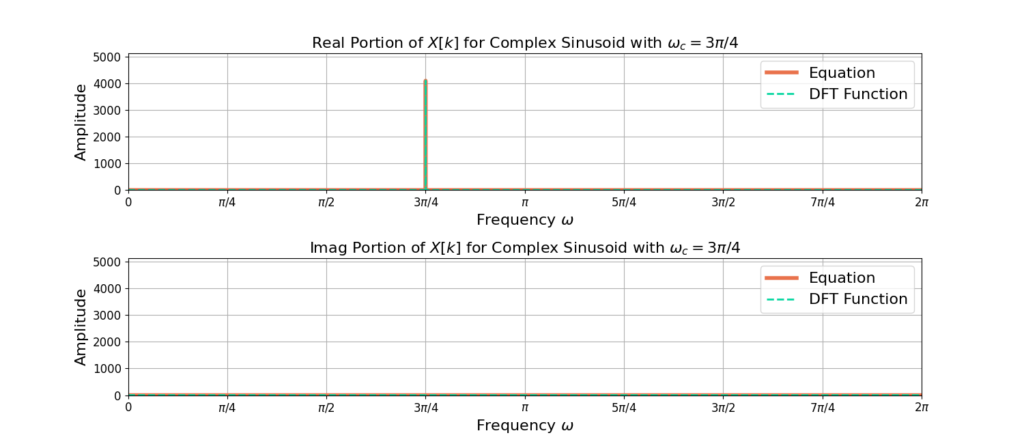
You may have noticed that all of the sinusoid’s energy is contained within a single bin when ![]() is of the form
is of the form ![]() as in Figures 1 and 2. For Figure 3, the energy is spread across multiple frequency bins. Figure 4 shows a zoomed in version of Figure 3 for more clarity.
as in Figures 1 and 2. For Figure 3, the energy is spread across multiple frequency bins. Figure 4 shows a zoomed in version of Figure 3 for more clarity.
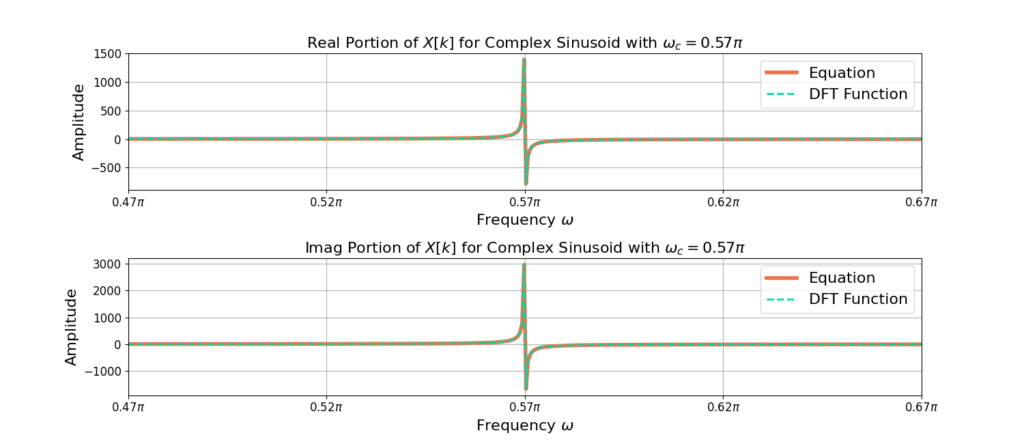
The sinusoid’s energy is spread across multiple bins because the sinusoid does not complete an integer number of cycles of frequency ![]() in N samples. This effect is related to the frequency resolution of the DFT.
in N samples. This effect is related to the frequency resolution of the DFT.
Conclusion
The discrete time Fourier transform (DTFT) and discrete Fourier transform (DFT) of a complex sinusoid were derived. The analytic equation was compared for correctness against a numerical DFT function.
Check out these other blogs:
![Figure 1: The two sequences for the autocorrelation of x0[n] and x0[n].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/5515-featured-125x100.png)
![Figure 3: The complex sinusoid e(j2 pi (2/4) n) only contains energy at X[2].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/8136-featured-125x100.png)
![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/15621-featured-125x100.png)