Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Bandwidth of a Moving Average Filter

August 3, 2022

Introduction

This blog shows how to approximate the 3 dB cutoff frequency of the moving average filter.

Check out these other blogs!

Moving Average Filter Impulse Response

The boxcar filter or boxcar window is an FIR filter whose weights are all 1:

(1) $\begin{equation*}h_{box}[n] = \begin{cases}1, & 0 \le n \le N-1 \\0, & \text{otherwise}.\end{cases}\end{equation*}$

The filter weights in (1) are normalized in the time domain to create a moving average (MA) filter

(2) $\begin{equation*}h_{ma}[n] = \begin{cases}1/N, & 0 \le n \le N-1 \\0, & \text{otherwise}.\end{cases}\end{equation*}$

Magnitude-Squared Frequency Response

The magnitude-squared of the frequency response for the boxcar window was derived in a previous blog,

(3) $\begin{equation*}\left| H_{box}\left( e^{j\omega} \right) \right|^2 = \frac{1 - \cos \left( \omega N \right)}{1 - \cos \left( \omega \right)}.\end{equation*}$

The moving average is normalized by a factor of 1/N therefore the magnitude-squared of the moving average is normalized by a factor of $1/N^2$ ,

(4) $\begin{equation*}\begin{split}\left| H_{ma}\left( e^{j\omega} \right) \right|^2 & = \frac{1}{N^2} \left| H_{box}\left( e^{j\omega} \right) \right|^2 \\& =\frac{1 - \cos \left( \omega N \right)}{N^2\left(1 - \cos \left( \omega \right)\right)}\end{split}\end{equation*}$

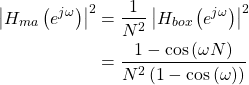
Gain at Zero-Frequency (omega=0)

There are multiple bandwidth definitions (see Bandwidth Measures). The focus of this blog is the half-power or 3 dB measure. The 3 dB bandwidth in decibels is

(5) $\begin{equation*}10\text{log}_{10}\left( 1/2 \right) \approx - 3~\text{dB}.\end{equation*}$

The moving average filter is a low-pass filter whose magnitude is the maximum value at $\omega = 0$ . Therefore to measure the half-energy point the maximum value has to be calculated, which is (4) at $\omega = 0$ ,

(6) $\begin{equation*}\begin{split}\left| H_{ma}\left( e^{j\omega} \right) \right|^2 |_{\omega=0} & = \frac{1 - \cos \left( 0 \right)}{N^2\left(1 - \cos \left( 0 \right)\right)} \\& = \frac{1}{N^2}. \\\end{split}\end{equation*}$

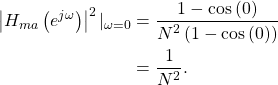
Finding the 3 dB Bandwidth

The 3 dB bandwidth is the frequency $\omega$ at which the magnitude-squared is 1/2 the maximum value,

(7) $\begin{equation*}\frac{1}{2} \left| H_{ma}\left( e^{j\omega} \right) \right|^2 |_{\omega=0} = \frac{1}{2N^2}.\end{equation*}$

After substituting (4) equation (7) can now be written as

(8) $\begin{equation*}\frac{1}{2N^2} = \frac{1 - \cos \left( \omega N \right)}{N^2\left(1 - \cos \left( \omega \right)\right)}\end{equation*}$

which is simplified to

(9) $\begin{equation*}\frac{1}{2} = \frac{1 - \cos \left( \omega N \right)}{1 - \cos \left( \omega \right)}.\end{equation*}$

Finding a closed-form solution for (9) is not trivial (see Wolfram’s solution when N=5), but the bandwidth can be approximated as approximately

(10) $\begin{equation*}\omega_{3dB} = \pi/N.\end{equation*}$

Figures 1-3 show the cutoff frequency approximation (10) for N=5, 10 and 16.

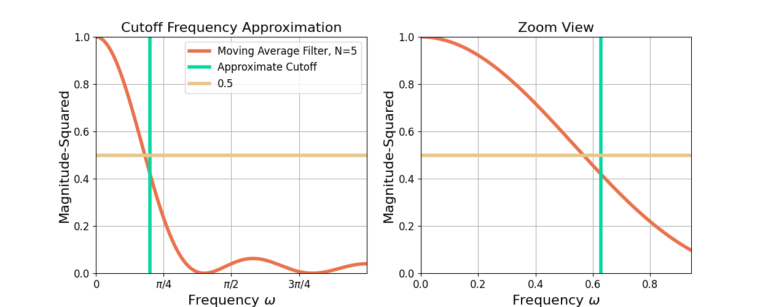
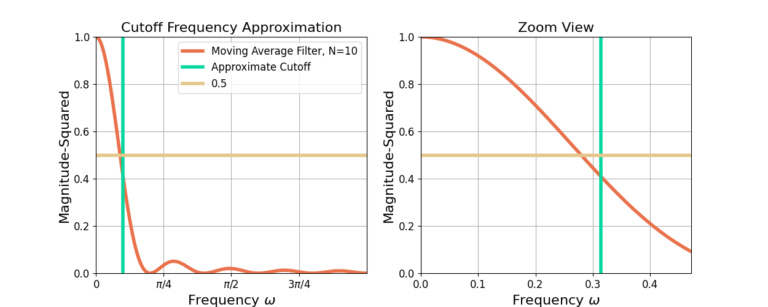
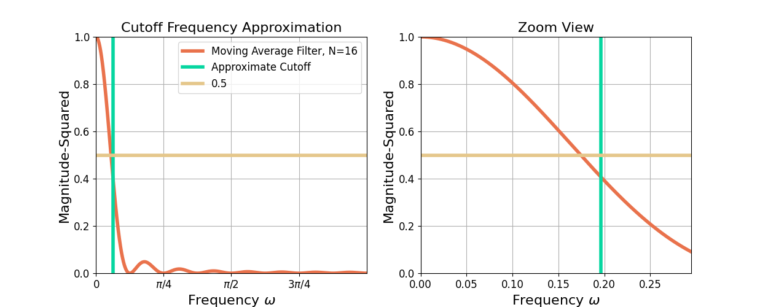
The cutoff approximation (10) is not an exact value for the frequency but it is a reasonable approximation.

Conclusion

The moving average filter is a normalized boxcar window or boxcar filter. The 3 dB point is where the magnitude-squared is 0.5. The 3 dB bandwidth of a moving average filter length N can be approximated by $\omega = \pi/N$ .

Check out these other blogs!

3 Responses

Curt says:

March 3, 2023 at 4:00 pm

This estimation approach can be used to determine the cutoff for a MA (lowpass) filter. What if I wanted to construct a MA bandpass filter from two lowpass filters? For example, if the filter length N based on the peak in the spectrum is 120 days, the low passband cutoff would be 38 days (3.14159/120=.02617, 1/.02617=38). Is there a way I cann use this estimation approach to determine the cutoff for the high passband of the MA bandpass filter?

Reply
WaveWalkerDSP says:

March 3, 2023 at 7:01 pm

> What if I wanted to construct a MA bandpass filter from two lowpass filters?

Are you required to use a moving average filter? It sounds like you are trying to build up a more sophisticated filter using the moving average as the foundation. I would be hesitant to do this, and I would design a band-pass filter using remez instead (see below).

The MA filter is a specific filter implementation where all of the taps are the same such that it computes the arithmetic mean of the input signal. It’s useful in some contexts but it doesn’t give you much control over the frequency response other than selecting the length N.

From what I can read into your question, it sounds like you need a band-pass filter in which you can specify the lower and upper cutoff frequency independently. If that’s the case I would design a band-pass filter with remez and skip the moving average filter. I have a blog here in which I describe how to do all of this using SciPy’s Remez function: https://www.wavewalkerdsp.com/2021/09/24/designing-fir-band-pass-filters-with-remez/

I hope this helps!

Reply
1. Curt A. Mitchell says:
  
  March 6, 2023 at 12:41 pm
  
  Great. I’ll take a look. Thanks.
  
  Reply