
Investing Time Into Younger Engineers
Introduction My career has been shaped and helped by those who invested in me. Pass it on by being a positive influence in the life
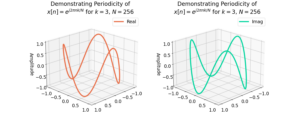
Why Does the DFT Need Windowing Functions?
Introduction The blog describes why windowing functions are needed in spectral analysis! This blog uses the Fourier Transform as a Cross-Correlation as a foundation and
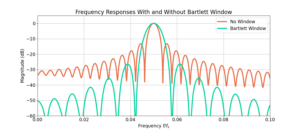
Windowing Functions for Better Spectral Analysis
Introduction The Discrete Time Fourier (DFT) and Fast Fourier Transform (FFT) are incredible tools for spectral analysis. Read on to find out why a windowing
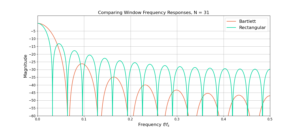
Bartlett (Triangular) Window Analysis With Python Code
Introduction An introduction to the Bartlett window: the impulse response is defined and a brief analysis of the frequency response as compared against the rectangular

The Value of Internships
Introduction Internships are an incredible way to gain experience and insight into industry while you are still in school. Read on to discover why internships
Celebrating 50,000 Page Views!
Just crossed 50,000 page views on May 9, 2023! Thank you everyone!

Discrete Fourier Transform (DFT) of Complex Sinusoid
Introduction This blog derives the frequency response of a complex sinusoid using the discrete Fourier transform (DFT). The derivation starts by apply the discrete time
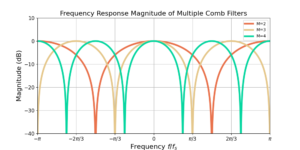
Comb Filter Introduction and Analysis
Introduction A comb filter is a multiplier-less filter, meaning it only uses additions when computing the impulse response. The comb filter is one of the
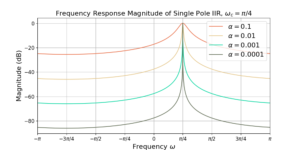
Band Pass Single Pole IIR Filter Design
Introduction A low-pass single pole infinite impulse response (IIR) filter is transformed into a band pass filter using simple mathematics! A previous blog described the
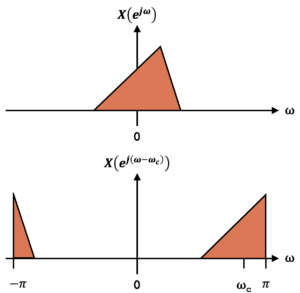
Complex Frequency Shifting in Discrete Time
Introduction Complex frequency shifting is the process of shifting a signal’s frequency response in the frequency domain. This blog describes how to apply complex frequency