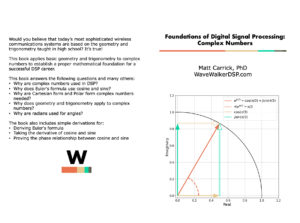
How to Create a LaTeX Paperback for Sale on Amazon
Table of Contents Introduction This blog post describes how to create a LaTeX paperback for sale on Amazon. Update: This book references images of the
Writing an eBook for Amazon Kindle with LaTeX on Linux
Table of Contents Introduction The following post is a map to avoid the traps and pitfalls of writing an eBook in LaTeX. I’ve compiled my
Cyclostationary and Stationary Processes with Examples
Introduction This blog describes stationary and cyclostationary processes using simple examples. A stationary process describes when a distribution does not change with time where as
Starting Small: Tips for Self Motivation for New Beginnings
Keep Going I cannot stop thinking about this tweet from @VisualizeValue and how incredible it is for self motivation: Keep going. pic.twitter.com/krKSUPRDbN — Visualize Value (@visualizevalue)
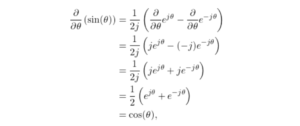
Derivative of Sine and Cosine Using Euler’s Formula
Introduction This posts shows how cosine and sine are related through their derivatives using Euler’s formula. I recall being presented with the derivative of sine
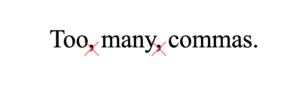
Stop Using Too Many Commas to be a Better Writer
Too many commas destroys the flow of a sentence. I know because I use too many commas. Each comma acts as a pause and too many commas makes good writing sound sluggish and boring.
The problem arises because I write as I’m thinking (I almost put a comma here!) and I put a comma when I need to take a thought break in the middle of sentence. However, you don’t want your reader to have a thought break. You want your reader to flow through your thoughts without a break in concentration. Using too many commas is an easy way to hamper otherwise excellent writing.
In writing the two paragraphs above I removed, or stopped myself from writing, 4-5 commas alone!
Oppenheim DSP Lectures YouTube Video Playlist
I recently came across a playlist on YouTube of Alan Oppenheim’s DSP lectures from 1975. Here’s the link to the playlist. Enjoy!
The Brand New Wave Walker DSP eBook!
The DSP eBook is on Amazon! Update! The eBook is #1 New Release in Signal Processing on Amazon! Currently the #1 New Release in Signal
![Figure 3: The complex sinusoid e(j2 pi (2/4) n) only contains energy at X[2].](https://www.wavewalkerdsp.com/wp-content/uploads/2022/01/DFTFrequencyResolutionExplained_4DFT_Freq2-300x134.png)
DFT Frequency Resolution Explained
Frequency resolution is defined as the ability to perfectly distinguish one frequency from another. The DFT frequency resolution is improved by increasing the signal length, not increasing the DFT size. The frequency resolution 
in radians of the DFT is
(1) 
where 
is the length of the input signal.
In this blog I demonstrate graphically and mathematically why and how increasing the signal length improves the frequency resolution, and why simply increasing the DFT size does not.
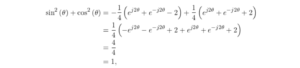
Trigonometric Identity: sin(x)^2 + cos(x)^2 = 1
In this post I derive a common trigonometric identity sin(x)^2 + cos(x)^2 = 1 using a form of Euler’s formula.