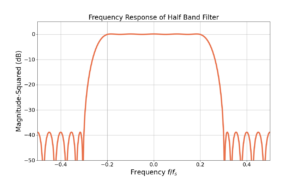
Half Band Filter Design Function in Python
The half band filter is an incredibly efficient filter useful in a number of applications as well as a great starting point for understanding fundamental DSP concepts. Previous posts covered the design of the filter weights and how to optimize the filter structure for computational efficiency. This blog posts simplifies the design of the half band filter weights using a Python function.
![Figure 1: The two sequences for the autocorrelation of x0[n] and x0[n].](https://www.wavewalkerdsp.com/wp-content/uploads/2021/11/correlationExplained_timeDomain_x0x0-300x188.png)
Cross Correlation Explained With Real Signals
Cross correlation mathematically measures the similarity of signals. Consider an example where you have a set of data samples represented by ![x[n]](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-94ce5deda23062dfdb5271c8c1471399_l3.png "Rendered by QuickLaTeX.com")
and ![y[n]](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-65d5680c3db2de15f6cc1bf673270c7d_l3.png "Rendered by QuickLaTeX.com")
. Cross correlation is used to measure on a sample by sample basis how similar is to . Simple examples with plots will demonstrate different combinations of positive, negative, strong and weak correlations.
1,000 Page Views!!!
It’s only been 94 days since launch and we just hit 1,000 page views! Thank you everyone!
And a very special thank you to Chad @ Cyclostationary.blog for linking to my site! Chad has published an incredible amount of DSP information on his blog and his expertise is off the charts. Cyclostationarity is a difficult subject and he describes the topic in a way that is much easier to understand than the academic literature. I particularly like his post on the Frequency Smoothing Method and the Time Smoothing Method. Please give him a look!
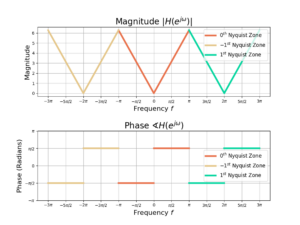
Derivative Filter Impulse Response Derivation
Sooner or later you’re going to have to apply a derivative to a discrete-time signal. An example would be building a derivative matched filter (DMF) for timing recovery [harris2021, p.490]. This brings us to our first piece of DSP Wisdom: If you need to do something in DSP it’s best to do it with a filter. So how do you build a derivative filter?
We’ll start with the derivation in continuous-time to make the math tractable then transform it into discrete-time. A follow-up post will discuss methods and alternatives for designing the derivative filter weights. Richard Lyons has a really great section on derivative filters in his textbook that is totally worth your time if you’re interested in more information on the topic [lyons2011, p.361].
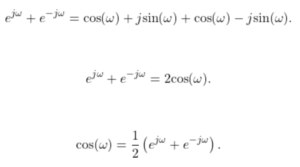
Using Euler’s Formula to Derive Sine and Cosine
Cosine and sine can be written as the sum of two complex exponentials.
Fourier Transform Convolution Property Derivation
The convolution property of the Fourier transform states that the convolution of 
and 
is the product of the frequency-responses 
and 
…
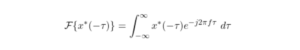
Fourier Transform Pairs of Conjugation and Time Reversal
Too often I find myself asking the questions “what is the Fourier transform of 
“? “What is the inverse Fourier transform of 
?” Finding them in a book or on Wikipedia often takes too long so to save myself the time and hopefully be useful to others, I’ve provided the derivations for the Fourier transforms of , 
, and 
below.
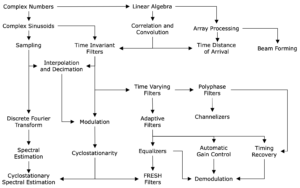
The DSP Family Tree: Grow Your Career
I recall being an undergraduate and wondering to myself “why are all of these things I am learning useful?” and “how are they going to be applied?” It is hard to have perspective when you’re in the trenches of your undergraduate or graduate degree to know the importance of the material you are learning. I have produced a DSP Family Tree which is my opinion on how all of the different sub-fields of DSP interact and build on one another.
My hope is that the DSP Family Tree is useful in motivating yourself that the concepts you are studying or have studied are important and can be built into larger things. You might also think of this as a road map: you can start with a destination and figure out what you need to learn along your journey.
![Figure 2: The complex sinusoid x0[n] = e(j2 pi 0.125 n) plotted in the complex plane.](https://www.wavewalkerdsp.com/wp-content/uploads/2021/10/aliasingSamplingCarTires_sinusoidsUnitCircleGrid0-300x50.png)
Aliasing, Sampling and Spinning Car Tires
You know how on car commercials sometimes it looks like the wheel is spinning backwards? How weird is that? The effect is called aliasing and it occurs when the wheel’s rotation rate is faster than twice the frame rate of the video camera. You can watch a video below that demonstrates aliasing on car tires as well as a video where it appears that a helicopter’s blades have stopped spinning due to a similar effect.
Square Root Raised Cosine Filter in Python
The square root raised cosine (SRRC) filter is used as a pulse shaping filter [harris2021, p.87] in many linear modulations such as BPSK, QPSK, and 16-QAM. Frustratingly neither SciPy or NumPy have a square-root raised cosine (SRRC) filter. Mathuranathan Viswanathan at GaussianWaves.com has a great post on how to build a square-root raised cosine filter. You can also find the design equations in [johnson2004, p.225, harris2021, p. 95].
I’ve written my own SRRC design script in Python which you can download from the WaveWalkerDSP GitHub page in the Blog Downloads repository.